本問題は，\(a, m, A_i\) 等を \(\gcd(a,m)\) で割ることにより，\(\gcd(a,m)=1\) の場合に帰着できます．以下の解説では \(\gcd(a,m)=1\) を仮定します．

---

[1] Grundy 数による言い換え

関数 \(G\colon \{0, 1, 2, \ldots \} \longrightarrow \{0, 1, 2, \ldots \}\) を以下によって帰納的に定義します．

• \(G(n) = \mathrm{mex}\{G(n-x)\mid x \in X, x\leq n\}\).

これは，数列が唯一の項 \(n\) からなる場合のゲームの Grundy 数です．本問題は次のように言い換えることができます．

添字 \(i\) と \(x\in X\) の組 \((i,x)\) であって，\(G(A_1)\oplus \cdots \oplus G(A_n) = G(A_i) \oplus G(A_i - x)\) を満たすものの個数を求めよ．

したがって，次の \(2\) つのことが行えれば，本問題を解くことができます．

• \(n\) が与えられたとき，\(G(n)\) を計算する．
• \(n, g\) が与えられたとき，\(G(n-x)=g\) を満たす \(x\in X\) の個数を求める．

---

[2] \(a=0\) の場合

\(\gcd(a,m)=1\) より \(m=1\) で，\(X = \{1,2,3,4,\ldots\}\) となります．この場合のゲームはニムと呼ばれるゲームと同一で，\(G(n) = n\) であることが簡単に分かります．

---

[3] マス目による状態表現

以下 \(a > 0\) を仮定します．整数の行番号，列番号を持つ縦横に無限に広がるマス目を考え， \(x\) 行 \(y\) 列にあるマスに数 \(mx+ay\) を対応させます．

例えば \(m=10, a=3\) の場合には，非負整数が対応するマスは以下の図のように並びます．

\(\gcd(a,m)=1\) より任意の非負整数がこのマス目に現れます．数の代わりにそれが対応するマスのひとつを考えることで，次のルールでマス目を移動するゲームについて各マスの Grundy 数を調べればよいです．

• あるマスからは，左方向に \(1\) マス・上方向に \(0\) マス以上進んだ位置に移動できる．

---

[4 - 1] \(0 < a \leq m/2\) の場合

次の手順により，各マスの Grundy 数を確定していくことができます．

step 1

左隣のマスが負の整数であるマスの Grundy 数は \(0\) である．

step 2

step 1 で \(0\) と確定した列の右隣の列に注目する．この列を特別な列と呼ぶことにする．特別な列のマスはこの時点で Grundy 数を求めることは難しいが，Grundy 数が \(1\) 以上であることだけは確定する．

step 3

特別な列の右隣の列の Grundy 数は，すべて \(0\) であることが分かる．その右隣の列のマスは Grundy 数は \(1\)，さらに右隣の列のマスは Grundy 数は \(0\) という要領で，次の特別な列に至るまでの列について Grundy 数が確定する．

step 4

ここまでで，特別な列を除くすべてのマスについて Grundy 数が確定している．\(a\leq m/2\) より 特別な列が \(2\) 列連続することはない．したがって，特別な列の左隣の列について既に Grundy 数が確定しているので，特別な列についても Grundy 数を確定できる．

---

[4 - 2] \(m/2 < a < m\) の場合

上隣のマスが負の整数であるようなマスを，上端のマスということにします．\(m/2 < a\) より，上端のマスは最大で \(2\) つまでしか真横に連続しません．また，\(a < m\) より上端のマスが \(2\) つ真横に連続する場所が存在します．

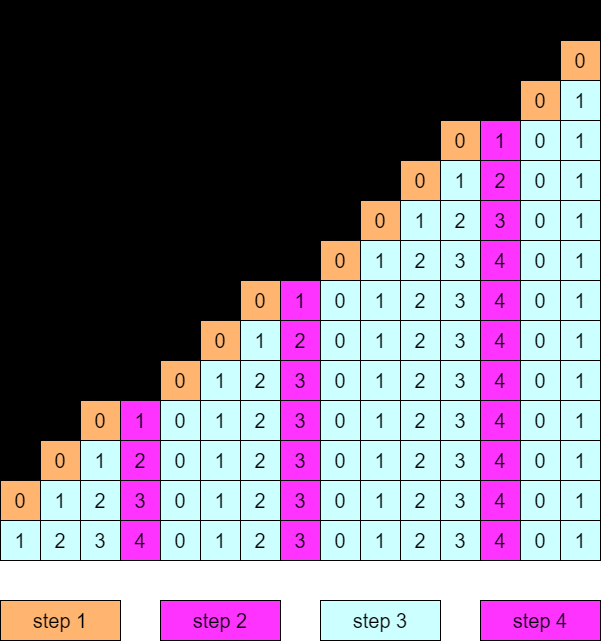
次の手順により，各マスの Grundy 数を確定していくことができます．

step 1

左隣のマスが負の整数であるマスの Grundy 数は \(0\) である．

step 2

上端のマスが真横に \(2\) つ並ぶ部分に注目し，そのうち右側のマスを含む列を特別な列と呼ぶことにする．特別な列のマスはこの時点で Grundy 数を求めることは難しいが，Grundy 数が \(1\) 以上であることだけは確定する．

step 3

特別な列の右隣の列の Grundy 数はすべて \(0\) であることが分かる．そこから右に進んでいくとき，次の特別な列に至るまで，上端のマスがひとつずつ上にずれていく．したがって列の Grundy 数の列は，

\[(0,0,0,0,0,0,\ldots)\to (0,1,1,1,1,1,\ldots)\to(0,1,2,2,2,2\ldots)\to (0,1,2,3,3,3,\ldots)\]

という規則で変化する．

step 4

ここまでで，特別な列を除いて，すべてのマスの Grundy 数が確定している．その左隣の列の Grundy 数は，\((0,1,2,3,3,3\ldots)\) というような規則になっており，特別な列の Grundy 数も \((1,2,3,4,4,4,\ldots)\) のような規則であることが分かる．

---

[5] まとめ

[2], [4-1], [4-2] を合わせると，すべての場合について Grundy 数の規則が解明できました．これらを利用すれば，

• \(n\) が与えられたとき，\(G(n)\) を計算する．
• \(n, g\) が与えられたとき，\(G(n-x)=g\) を満たす \(x\in X\) をの個数を求める．

という計算を行うことも難しくはありません．あるマスと上端や左端などの位置関係も，\(m\) や \(a\) で割った余りの計算を利用すれば計算できます．

これらの計算は \(O(1)\) 時間で行うことができ，本問題は全体として \(O(N)\) 時間で解くことが出来ます．