Official

E - Christmas Wreath Editorial by evima

There was just one sample input with \(N = 4\), for which the answer is No, so you might have doubted the existence of a valid decoration. However, there is one if \(N\) is \(6\) or greater and \(N \mod 3\) is \(0\) or \(1\).


Table of contents

The solution to the problem has two steps.

  • In Step 1, we find a pattern of the decoration that is guaranteed to satisfy Condition 2 (there is no triangle with three differently colored ropes).
  • In Step 2, from the decorations in the pattern above, we find one that also satisfies Condition 1 (there are equal numbers of red, blue, and white ropes).

These steps are explained in Sections 1 and 2. Especially, we have three solutions for Step 2. The subsequent sections are:

  • Section 3: Summary
  • Section 4: Sample Implementations (C++ and Python)
  • Section 5: Bonus

If you are in a hurry, go to Section 3.


Step 1. Fixing the pattern

We need to make a decoration that satisfies the two conditions:

Condition 1: there are equal numbers of red, blue, and white ropes,

Condition 2: there is no triangle with three differently colored ropes.

Condition 2 particularly looks complicated, but undergoing the following procedure guarantees that this condition is satisfied.

Let $\langle a, b \rangle$ denote the rope connecting Balls $a$ and $b$.
  • Phase 1: Choose some color and light up $\langle 1, 2 \rangle$ in that color.
  • Phase 2: Choose some color and light up all of $\langle 1, 3 \rangle, \langle 2, 3 \rangle$ in that color.
  • Phase 3: Choose some color and light up all of $\langle 1, 4 \rangle, \langle 2, 4 \rangle, \langle 3, 4 \rangle$ in that color.
  • $\vdots$
  • Phase $N-1$: Choose some color and light up all of $\langle 1, N \rangle, \langle 2, N \rangle, \langle 3, N \rangle, \dots, \langle N-1, N \rangle$ in that color.

For example, when \(N = 5\), choosing red, red, white, blue in this order makes the decoration below. As you can see, there is no triangle with three different ropes.

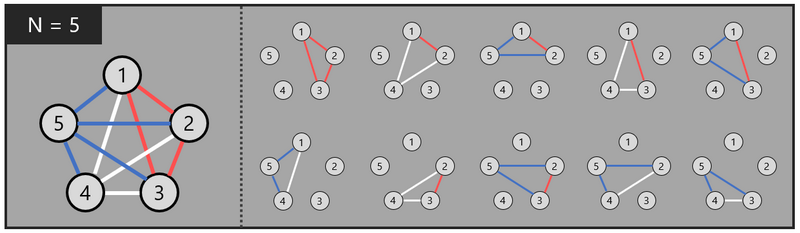
Why does this procedure guarantee that Condition 2 is satisfied? Because:

  • Let \(a, b, c \ (1 \leq a \lt b \lt c \leq N)\) be the balls that are the vertices of a triangle.
  • Because \(\langle a, c \rangle\) and \(\langle b, c \rangle\) are lighted in the same phase \(c-1\), they have the same color.
  • Therefore, the colors of the three ropes are never all different.

Of course, there can be other ways to make a decoration that satisfies both conditions. However, even if we limit ourselves to using this pattern, we can make a valid decoration for all \(N\) where the answer is Yes (more specifically, all \(N\) at least \(6\) such that \(N \mod 3\) is \(0\) or \(1\); see Section 2-3 for proof).


Step 2. Find one with equal numbers of red, blue, white ropes

The procedure described in Step 1 guarantees that the decoration satisfies Condition 2. The other condition is:

Condition 1: There are equal numbers of red, blue, and white ropes.

Can we decide the color in Phase \(1, 2, \dots, N-1\) to satisfy this?

For example, in the previous example with \(N = 5\), after choosing red, red, white, blue in this order, we have:

  • \(1 + 2 = 3\) red ropes (because red is chosen in Phases \(1, 2\)),
  • \(4\) blue ropes (because blue is chosen in Phases \(4\)),
  • \(3\) white ropes (because white is chosen in Phases \(3\)).

As seen here, the number of ropes in each color is equal to the sum of the “phase numbers” where that color is chosen. Thus, Condition 1 is satisfied when

\(1, 2, 3, \dots, N-1\) are divided into three groups so that the sums are equal.

Here are some examples.

  • When \(N = 6\): we can divide \(1, 2, 3, 4, 5\) into the groups \(\{1, 4\}, \{2, 3\}, \{5\}\), where all sums are \(5\).
  • When \(N = 9\): we can divide \(1, 2, 3, 4, 5, 6, 7, 8\) into the groups \(\{1, 2, 3, 6\}, \{4, 8\}, \{5, 7\}\), where all sums are \(12\).

For instance, in the case \(N = 6\), we can choose red in Phases \(1, 4\), blue in Phases \(2, 3\), white in Phase \(5\) to satisfy both conditions.

Now, how do we divide \(1, 2, 3, \dots, N-1\) into three groups with equal sums? We will describe three methods:

  • Randomized algorithm
  • Dynamic Programming (DP)
  • Mathematical construction


2-1. Randomized algorithm

There may not be many participants who did it this way, but the following algorithm can easily find a solution.

  • 1. Using RNG, randomly assign each of \(1, 2, 3, \dots, N-1\) to one of the three groups.
  • 2. If the sums of the numbers in the three groups are all equal, we have found a solution. Otherwise, start over.
  • 3. If no solution is found for some duration of time, assume that the answer is No.

Some may suspect that such a miracle of having three equal sums in Phase 2 is rare, but it is fast enough for the values of \(N\) not greater than \(50\) where the answer is Yes.


2-2. Dynamic Programming (DP)

We can use DP to determine if there is a division with three equal sums.

To satisfy the conditions:

  • The sum of the numbers in Group 1 must be \(\frac{N(N-1)}{6}\).
  • The sum of the numbers in Group 2 must be \(\frac{N(N-1)}{6}\).
  • (Then, the sum of the numbers in Group 3 will automatically be \(\frac{N(N-1)}{6}\).)

Now, let us compute the following values with DP, in ascending order of \((i, sum1, sum2)\).

\(dp[i][sum1][sum2]\): whether it is possible to make the sum of the numbers in Group 1 \(sum1\) and that in Group 2 \(sum2\) (true or false)

Eventually, if \(dp[N-1][\frac{N(N-1)}{6}][\frac{N(N-1)}{6}]\) is true, there is a desirable division; if it is false, there is no such division.

Since there are \(O(N^5)\) states \((i, sum1, sum2)\), the complexity is \(O(N^5)\). For your reference, this is the subset sum problem expanded to two dimensions.

bool dp[51][393][393]; // assume that p[i][j][k] are all initialized to 0
int A = N * (N - 1) / 6; // not divisible when N = 3k+2, in which case the answer is No

dp[0][0][0] = true
for (int i = 1; i <= N - 1; ++i) {
	for (int sum1 = 0; sum1 <= A; ++sum1) {
		for (int sum2 = 0; sum2 <= A; ++sum2) {
			if (sum1 >= i && dp[i - 1][sum1 - i][sum2] == true) {
				dp[i][sum1][sum2] = true; // put i in Group 1
			}
			if (sum2 >= i && dp[i - 1][sum1][sum2 - i] == true) {
				dp[i][sum1][sum2] = true; // put i in Group 2
			}
			if (dp[i - 1][sum1][sum2] == true) {
				dp[i][sum1][sum2] = true; // put i in Group 3
			}
		}
	}
}

After computing the values in the DP table, we can trace \((i, sum1, sum2)\) backward to find the actual grouping.


2-3. Mathematical construction

Without using a randomized algorithm or dynamic programming, we can mathematically form a grouping based on induction.

When \(N = 3k+2\) (\(k\) is an integer), the sum of \(1, 2, \dots, N-1\) is not a multiple of \(3\), so there is no grouping with equal sums. When \(N = 3, 4\), there is no such grouping, either.

Now, we will consider the remaining case. First, let us make one grouping with equal sums for each of \(N = 6, 7, 9, 10\).

  • When \(N = 6\): Divide \(1, 2, 3, 4, 5\) into \(\{1, 4\}, \{2, 3\}, \{5\}\).
  • When \(N = 7\): Divide \(1, 2, 3, 4, 5, 6\) into \(\{1, 6\}, \{2, 5\}, \{3, 4\}\).
  • When \(N = 9\): Divide \(1, 2, 3, 4, 5, 6, 7, 8\) into \(\{1, 2, 3, 6\}, \{4, 8\}, \{5, 7\}\). (Other solutions exist.)
  • When \(N = 10\): Divide \(1, 2, 3, 4, 5, 6, 7, 8, 9\) into \(\{1, 2, 3, 4, 5\}, \{6, 9\}, \{7, 8\}\). (Other solutions exist.)

Based on them, we can form groupings for \(N = 12, 13, 15, 16, 18, 19, \dots\), as follows.

  1. Let $n = N$ initially, and repeat the following until $n \lt 12$.
    • Add $\{n-6, n-1\}$ to Group 1, $\{n-5, n-2\}$ to Group 2, $\{n-4, n-3\}$ to Group 3.
    • Then, decrease $n$ by $6$.
  2. Eventually, $n$ becomes $6$, $7$, $9$, or $10$. To each group, add the corresponding numbers in the grouping for $N = n$ (see above).

For example, when \(N = 21\), we get the grouping \(\{1, 2, 3, 6, 9, 14, 15, 20\}, \{4, 8, 10, 13, 16, 19\}, \{5, 7, 11, 12, 17, 18\}\), where the sums are all equal.


3. Summary

The problem can be solved as follows.

  • For each \(i \ (2 \leq i \leq N)\), we light up \(\langle 1, i \rangle, \langle 2, i \rangle, \dots, \langle i-1, i \rangle\) in the same color. Then, Condition 2 (there is no triangle with three differently colored ropes) is always satisfied.
  • Now, finding a way to satisfy Condition 1 (there are equal numbers of red, blue, and white ropes) is equivalent to finding a division of \(1, 2, \dots, N-1\) into three groups with equal sums.
  • To find this grouping, we can use the following three methods.
    • Randomized algorithm
    • Dynamic programming
    • Mathematical construction

Here, \(\langle a, b \rangle\) denote the rope connecting Balls \(a, b\).

Particularly, in Mathematical construction, * the groupings for \(N = 6, 7, 9, 10\) can be found by hand; * the groupings for \(N \geq 12\) can be found inductively by adding \(\{N-6, N-1\}, \{N-5, N-2\}, \{N-4, N-3\}\) to the grouping when \(N\) is \(6\) smaller.

As a result, a desirable decoration exists when \(N = 6, 7, 9, 10, 12, 13, 15, 16, 18, 19, \dots\)

4. Sample Implementations (C++ and Python)

Below are C++ implementations of the three approaches.

Below are Python implementations of the three approaches.


5. Bonus

Actually, we can use hill climbing to solve this problem.

Here is a sketch of this technique:

  1. Generate a random solution \(X\).
  2. Repeat the following:
    • Slightly modify some parts of \(X\) randomly. Let \(X'\) be the result. (For example, choose two values randomly and swap them.)
    • If \(X'\) is “better” than \(X\), update \(X\) to \(X'\).
  3. After enough iterations, the solution should be improved to some extent.

We can apply hill climbing to this problem, too.


Hill climbing in this problem

We need to make a decoration where the ropes of each triangle have different colors.

To handle this, let us define the score of a decoration as the number of triples \((a, b, c)\) such that the colors of \(\langle a, b \rangle, \langle b, c \rangle, \langle c, a \rangle\) are all different. When the numbers of red, blue, white ropes are equal, and the score is \(0\), we have a desirable decoration.

Now, consider the following algorithm with hill climbing.

  1. First, make a random decoration with \(N(N-1)/6\) red, \(N(N-1)/6\) blue, \(N(N-1)/6\) white ropes.
  2. Repeat the following enough times.
    • From the \(N(N-1)/2\) ropes, choose two randomly and swap their colors.
    • Compute the score of this new decoration. If it is higher (worse) than it was, redo the swap.
  3. When the score is \(0\), we have found an answer.

This simple algorithm can solve the problem without creative observations, such as finding the pattern in Step 1.

However, since there are \(O(N^3)\) triangles, naive computation of the score takes \(O(N^3)\) time, which might be too slow to perform enough iterations with bad luck. Can we make it faster?

Actually, swapping two ropes affects the colors of at most \(2N-4\) triangles, because swapping \(\langle a, b \rangle\) and \(\langle c, d \rangle\) only affects the triangles whose vertices are \((a, b, x)\) or \((c, d, x)\).

Therefore, we can compute the change of the score by checking just these \(2N-4\) triangles to accelerate each iteration of hill climbing, making the program very fast under the constraint \(N \leq 50\).


Hill Climbing and AtCoder Heuristics Contest (AHC)

Starting on March 2021, AtCoder holds AHC. In these contests, unlike the usual ones such as ARC, participants are asked to find as good solutions as possible in a problem where finding the optimal solution is unrealistic.

Hill climbing, which can often produce decent solutions despite being simple, is used in many AHCs.

Simulated annealing, a probabilistic variant of hill climbing, is often used, too. Hill climbing never updates a solution to a worse one, but simulated annealing also adopts a worse solution probabilistically, according to the degree to which the solution is worsened.

In addition to heuristics contests such as AHC, hill climbing and simulated annealing can occasionally be used in algorithm contests such as ARC.

posted:
last update: