Editorial - AtCoder Regular Contest 131

Contest Duration: 2021-12-05 21:00:00+0900 - 2021-12-05 23:00:00+0900 (local time) (120 minutes) Back to Home

Official

E - Christmas Wreath Editorial by square1001

本コンテストの問題 E「Christmas Wreath」の解説です。

この問題は、入力例が $N = 4$ しかなく、これも答えが No であるため、本当に条件を満たすクリスマス飾りがあるのかと疑った方も多いでしょう。しかし、$N$ が $6$ 以上の $3$ で割って $0$ か $1$ 余る数ならば、適切なクリスマス飾りを構成できるのです。

では、解説を始めましょう。

解説の目次

この問題の解法は 2 ステップに分かれます。

ステップ 1 では、条件 2（3 辺の色がすべて異なる三角形が存在しない）を確実に満たすようなクリスマス飾りの作り方の「パターン」を見つけます。
ステップ 2 では、この作り方の「パターン」のなかで 条件 1（赤・青・白の個数が同じ）も満たすようなものを探します。

これらの解法のステップは、それぞれ 1 節と 2 節で解説します。特にステップ 2 は、3 通りの解法を紹介します。それ以降の解説では、

3 節：解法のまとめ
4 節：実装例 (C++, Python)
5 節：おまけ

について書きます。なお、急いで解説を読みたい方は、3 節「解法のまとめ」を読んでください。

ステップ 1. クリスマス飾りの「パターン」を決める

まず、この問題では

条件 1：赤・青・白の個数が同じ

条件 2：3 辺の色がすべて異なる三角形が存在しない

という 2 つの条件を満たすクリスマス飾りを作らなければなりません。特に 条件 2 は複雑に見えますが、実は次のような作り方をすれば必ずこの条件を満たします。

次のような手順でクリスマス飾りを作る。ただし、ボール $a, b$ を結ぶロープを $\langle a, b \rangle$ と表す。

フェーズ 1：適当に色を選び、ロープ $\langle 1, 2 \rangle$ をその色で点灯する

フェーズ 2：適当に色を選び、ロープ $\langle 1, 3 \rangle, \langle 2, 3 \rangle$ を全てその色で点灯する

フェーズ 3：適当に色を選び、ロープ $\langle 1, 4 \rangle, \langle 2, 4 \rangle, \langle 3, 4 \rangle$ を全てその色で点灯する

（中略）

フェーズ $N-1$：適当に色を選び、ロープ $\langle 1, N \rangle, \langle 2, N \rangle, \langle 3, N \rangle, \dots, \langle N-1, N \rangle$ を全てその色で点灯する

例えば、$N = 5$ で、各フェーズで色を「赤・赤・白・青」の順番で選ぶと、次のようなクリスマス飾りができます。見てのとおり、どの三角形を選んでもロープがすべて異なる色ではありません。

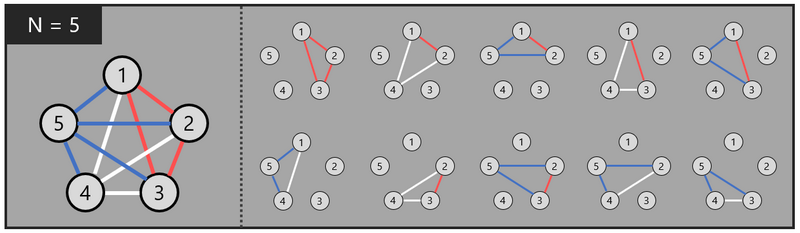
なぜ、このような作り方をすれば、条件 2 を必ず満たすのでしょうか？この理由は次の通りです。

三角形の頂点をなすボールの番号を $a, b, c \ (1 \leq a \lt b \lt c \leq N)$ とする
ロープ $\langle a, c \rangle$ とロープ $\langle b, c \rangle$ は同じフェーズ $c-1$ で点灯したから、同じ色である
したがって、3 つのロープの色がすべて異なることはない

もちろん、この作り方以外でも条件 1・2 を両方満たすクリスマス飾りを作れる場合はあります。しかし、この作り方の「パターン」に限定しても、答えが Yes となるすべての $N$（具体的には、$3$ で割って $0$ か $1$ 余る $6$ 以上の数）に対してクリスマス飾りを作ることができます（この理由は 2-3 項を見てください）

ステップ 2. 赤・青・白のロープが同数の作り方を見つける

ステップ 1 で説明した「パターン」のクリスマス飾りを作れば、必ず 条件 2 を満たします。残った条件は：

条件 1：赤・青・白のロープの数は等しい

です。さて、フェーズ $1, 2, \dots, N-1$ で点灯する色をうまく決めることで、条件 1 を満たすものを作れるでしょうか？

例えば、先ほどの $N = 5$ の例で、各フェーズで色を「赤・赤・白・青」の順番で選ぶと

赤いロープ：$1 + 2 = 3$ 個（フェーズ $1, 2$ で選んだから）
青いロープ：$4$ 個（フェーズ $4$ で選んだから）
白いロープ：$3$ 個（フェーズ $3$ で選んだから）

このように、各色のロープの本数を計算してみると、選んだフェーズ番号の合計になっています。だから、条件 1 を満たすのは

$1, 2, 3, \dots, N-1$ を、合計が等しくなるように 3 つのグループに分ける

ときになるのです。さて、具体例をいくつかあげてみましょう。

$N = 6$ のとき：$1, 2, 3, 4, 5$ を 3 つのグループ $\{1, 4\}, \{2, 3\}, \{5\}$ に分ける。合計はすべて $5$ で等しい。
$N = 9$ のとき：$1, 2, 3, 4, 5, 6, 7, 8$ を 3 つのグループ $\{1, 2, 3, 6\}, \{4, 8\}, \{5, 7\}$ に分ける。合計はすべて $12$ で等しい。

例えば $N = 6$ のときは、フェーズ $1, 4$ で赤、フェーズ $2, 3$ で青、フェーズ $5$ で白を選ぶと、条件 1・2 を両方満たすクリスマス飾りが作れるのです！

さて、$1, 2, 3, \dots, N-1$ を合計が等しくなるように 3 グループに分けるためにはどんな方法があるのでしょうか？本解説では 3 通りの方法を解説したいと思います。

乱択アルゴリズムを使った方法
動的計画法 (DP) を使った解法
数学的な構成方法

2-1. 乱択アルゴリズムを使った解法

この方法でやった人はあまり多くないと思いますが、実は次のようなアルゴリズムで簡単に答えを出すことができます。

ステップ 1：$1, 2, 3, \dots, N-1$ を順に、乱数を使ってランダムに 3 つのグループのいずれかに割り当てる。
ステップ 2：グループに入った数の合計がすべて等しければ、これで答えが求まった。等しくなければ、もう一度最初からやり直す。
ステップ 3：一定時間ループを回しても答えが求まらなかったら、答えは No であるとみなす。

「ステップ 2 で合計が等しくなる奇跡なんてそう起こらないのではないか」と思う方もいるかもしれません。しかし実は、答えが Yes となるような $50$ 以下の $N$ に対しては、十分高速に答えを出すことができます。

このように、乱数を使うことで答えを得るアルゴリズムを「乱択アルゴリズム」といいます。興味のある方はぜひ調べてみましょう。

2-2. 動的計画法 (DP) を使った解法

動的計画法 (DP) を使うと、合計が等しくなるようなグループ分けが存在するかどうか判定できます。

条件を満たすためには

グループ 1 に入る数の合計を $\frac{N(N-1)}{6}$ にする
グループ 2 に入る数の合計を $\frac{N(N-1)}{6}$ にする
（すると、グループ 3 に入る数の合計は自動的に $\frac{N(N-1)}{6}$ になる）

であることが必要です。ここで、次の値を $(i, sum1, sum2)$ の小さい順に DP で計算していくことにします。

$dp[i][sum1][sum2]$：$1, 2, \dots, i$ をグループに割り当てた時点で、グループ 1 の数の合計を $sum1$、グループ 2 の数の合計を $sum2$ にすることが可能か（可能なら true、不可能なら false）

最終的に $dp[N-1][\frac{N(N-1)}{6}][\frac{N(N-1)}{6}]$ が true ならば適切なグループ分けが存在し、false ならば存在しないことになります。

$(i, sum1, sum2)$ の状態数が $O(N^5)$ 通りあるので、計算量は $O(N^5)$ です。なお、これは部分和問題の 2 次元への拡張になっています。

bool dp[51][393][393]; // 説明の都合上、dp[i][j][k] はすべて false で初期化されているとする
int A = N * (N - 1) / 6; // N = 3k+2 と表せる場合 N * (N - 1) / 6 は割り切れないので、答えは false なことに注意

dp[0][0][0] = true
for (int i = 1; i <= N - 1; ++i) {
	for (int sum1 = 0; sum1 <= A; ++sum1) {
		for (int sum2 = 0; sum2 <= A; ++sum2) {
			if (sum1 >= i && dp[i - 1][sum1 - i][sum2] == true) {
				dp[i][sum1][sum2] = true; // i をグループ 1 に入れる場合
			}
			if (sum2 >= i && dp[i - 1][sum1][sum2 - i] == true) {
				dp[i][sum1][sum2] = true; // i をグループ 2 に入れる場合
			}
			if (dp[i - 1][sum1][sum2] == true) {
				dp[i][sum1][sum2] = true; // i をグループ 3 に入れる場合
			}
		}
	}
}

DP の値を計算し終わった後、$(i, sum1, sum2)$ を逆順にたどることで解を復元する「DP 復元」というテクニックを使うと、実際のグループ分けを求められます。DP 復元について知らない方は、drken1215 さんの記事を見てください。

2-3. 数学的な構成方法

実は、乱択アルゴリズムや動的計画法を使わなくても、帰納法をベースとした数学的な方法でもグループ分けを作ることができます。

$N = 3k+2$（$k$ は整数）と表せるとき、$1, 2, \dots, N-1$ の合計が $3$ の倍数にならないので、合計が等しくなるグループ分けはできません。また、$N = 3, 4$ のときも、そのようなグループ分けはありません。

では、残りの場合を考えてみましょう。まず、$N = 6, 7, 9, 10$ の場合の、合計が等しくなるグループ分けを 1 つ作ってみましょう。

$N = 6$ のとき：$1, 2, 3, 4, 5$ を 3 つのグループ $\{1, 4\}, \{2, 3\}, \{5\}$ に分ける
$N = 7$ のとき：$1, 2, 3, 4, 5, 6$ を 3 つのグループ $\{1, 6\}, \{2, 5\}, \{3, 4\}$ に分ける
$N = 9$ のとき：$1, 2, 3, 4, 5, 6, 7, 8$ を 3 つのグループ $\{1, 2, 3, 6\}, \{4, 8\}, \{5, 7\}$ に分ける（他にもいくつか方法があります）
$N = 10$ のとき：$1, 2, 3, 4, 5, 6, 7, 8, 9$ を 3 つのグループ $\{1, 2, 3, 4, 5\}, \{6, 9\}, \{7, 8\}$ に分ける（他にもいくつか方法があります）

これをベースとして、$N = 12, 13, 15, 16, 18, 19, \dots$ のときのグループ分けを作ることができます。$N \geq 12$ のときも

最初 $n = N$ として、$n \lt 12$ になるまで以下を繰り返す

グループ 1 に $\{n-6, n-1\}$、グループ 2 に $\{n-5, n-2\}$、グループ 3 に $\{n-4, n-3\}$ を追加する
その後、$n$ を $6$ 減らす

最終的に $n$ は $6, 7, 9, 10$ のいずれかになるので、$N = n$ のときのグループ分け（上を参照）を各グループに追加する

という方法でグループ分けを作れます。

例えば $N = 21$ のとき、$\{1, 2, 3, 6, 9, 14, 15, 20\}, \{4, 8, 10, 13, 16, 19\}, \{5, 7, 11, 12, 17, 18\}$ というグループ分けが得られて、この合計はすべて等しくなっています。

3. 解法のまとめ

まとめると、次のような方針でこの問題を解けます。

各 $i \ (2 \leq i \leq N)$ に対して、ロープ $\langle 1, i \rangle, \langle 2, i \rangle, \dots, \langle i-1, i \rangle$ を同じ色で点灯させると、必ず 条件 2（3 辺の色がすべて異なる三角形が存在しない）を満たす
すると、条件 1（赤・青・白のロープの数は等しい）を満たす方法を求める問題は、$1, 2, \dots, N-1$ を合計が等しくなるような 3 グループに分ける問題になる
このグループ分けは、次の 3 通りの方法で求められる
- 乱択アルゴリズムを使った方法
- 動的計画法 (DP) を使った方法
- 数学的な構成方法

ただし、ボール $a, b$ を結ぶロープを $\langle a, b \rangle$ と表します。

特に「数学的な構成方法」を使う場合は

$N = 6, 7, 9, 10$ のときのグループ分けは手計算で求める
$N \geq 12$ のときのグループ分けは、$N$ が $N-6$ のときのグループ分けに $\{N-6, N-1\}, \{N-5, N-2\}, \{N-4, N-3\}$ を追加することで帰納的に得られる

となります。結果として、条件を満たすクリスマス飾りが存在するのは $N = 6, 7, 9, 10, 12, 13, 15, 16, 18, 19, \dots$ のときです。

4. 実装例 (C++, Python)

C++ による 3 種類の解法それぞれの実装例です。

乱択アルゴリズムによる解法：https://atcoder.jp/contests/arc131/submissions/27697585
動的計画法による解法：https://atcoder.jp/contests/arc131/submissions/27697706
数学的な構成方法：https://atcoder.jp/contests/arc131/submissions/27697752

Python による 3 種類の解法それぞれの実装例です。

乱択アルゴリズムによる解法：https://atcoder.jp/contests/arc131/submissions/27697896
動的計画法による解法：https://atcoder.jp/contests/arc131/submissions/27698083
数学的な構成方法：https://atcoder.jp/contests/arc131/submissions/27698092

5. おまけ

実は、この問題は山登り法を使って解くこともできます。

「山登り法って何？」と思う方も多いと思うので、アイデアを説明します。山登り法は、次のようなアイデアを用いたアルゴリズムです。

適当な解 $X$ を生成する
以下の処理を繰り返す
- 解 $X$ の一部をランダムに変化させたものを $X'$ とする（例：ランダムに 2 つの値を選んで交換するなど）
- $X$ よりも $X'$ の方が「良い解」であれば、$X$ を $X'$ に更新する
十分な回数繰り返せば、ある程度良い解が作れているはず

この問題にも山登り法を適用することができます。

山登り法を使ってみよう

この問題では、3 辺がすべて異なるようにクリスマス飾りを作らなければなりません。

ここで、クリスマス飾りの スコア を「ロープ $\langle a, b \rangle, \langle b, c \rangle, \langle c, a \rangle$ の色がすべて異なるような $(a, b, c)$ の組の数」とします。赤・青・白のロープが同数で、スコアが 0 になれば、正解となります。

ここで、次の山登り法にアルゴリズムを考えます。

最初に、赤・青・白のロープの数がそれぞれ $N(N-1)/6$ 個となるようなクリスマス飾りを適当に作る
以下の処理を十分な回数繰り返す
- $N(N-1)/2$ 本のロープの中からランダムに $2$ 本選び、この色を交換する。
- 新しいクリスマス飾りのスコアを求め、これが元々より高ければ（スコア 0 から遠くなるので）交換を元に戻す。
スコアが 0 になれば、答えが求まった

このような単純なアルゴリズムで、ステップ 1 の作り方の「パターン」のような発想を思いつかなくても、正解することができます。

実装例 (C++)：https://atcoder.jp/contests/arc131/submissions/27709349

しかし、三角形は $O(N^3)$ 個あるので、2. で計算量 $O(N^3)$ かけてスコアを求めていると時間がかかってしまい、十分な回数のループを繰り返すことができない場合もあります。さらに高速にできないでしょうか。

実は、2 本のロープを交換して色が変わる三角形は高々 $2N-4$ 個しかありません。なぜなら、ロープ $\langle a, b \rangle, \langle c, d \rangle$ を交換したとすると、$(a, b, x)$ または $(c, d, x)$ を 3 頂点とする三角形以外は何も変化しないからです。

したがって、これらの $2N-4$ 個の三角形を見るだけで「スコアがいくつ増加／減少したか」を調べることができ、高速に山登り法の 1 回のループを終えることができ、$N \leq 50$ の制約では非常に短時間で答えを出すことができます。

山登り法とヒューリスティクスコンテスト (AHC)

2021 年 3 月以降、AtCoder は「AtCoder Heuristics Contest (AHC)」を開催しています。AHC は、普段の ARC などとは異なり、「最適解が得られないような問題で、できるだけ良い解を求めるプログラムを書いて競う」という形式の問題が出題されます。

山登り法は、方法が単純なのにもかかわらずそれなりに良い解を出せることが多く、AHC の多くのコンテストの解法として使われます。

また、山登り法に確率要素を加えた焼きなまし法もよく使われます。山登り法では解が悪化する方向に進めることは絶対にないですが、焼きなまし法では、解が悪化する場合でも、どのくらい悪化するかに応じて確率で解を更新するかどうかを決めます。

山登り法と焼きなまし法は AHC などのヒューリスティクスコンテストで使われるのはもちろん、ARC のようなアルゴリズムコンテストでも使える場合があるので、ぜひ覚えておきましょう。

posted:
last update: