D - Inc, Dec - Decomposition Editorial
by  maspy
maspy
\(2\) つの解法を解説します。
- DP の高速化として得られる \(\Theta(N\log N)\) 時間計算量での解法:この解説
- 最適解の構造を調べることで得られる \(\Theta(N)\) 時間計算量での解法:https://atcoder.jp/contests/arc123/editorial/2292
◆ 問題の整理
\(2n\) 個の整数 \(B_i, C_i\) を上手く定める問題ですが、\(B_i\) を定めると \(C_i\) は自動的に定まるため、 \(n\) 個の整数を定める問題へと言い換えることができます。
結局、次の形の問題が解ければよいことが分かります:
- 定数 \(a_i, b_i\) が与えられる。
- 整数 \(x_1, x_2, \ldots, x_N\) を、\(x_i + a_i \leq x_{i+1}\) が成り立つように定めるとき、\(\sum |x_i| + |x_i - b_i|\) の最小値を求めよ。
以下の解説でも、同じ記号 \(x_i, a_i, b_i\) を用いていきます。
◆ DP による計算式
\(x_1, \ldots, x_n\) を \(x_i + a_i \leq x_{i+1}\) かつ \(x_n = x\) となるように定めるとき、\(\sum_{1\leqq i\leqq n}\bigl(|x_i| + |x_i-b_i|\bigr)\) としてありうる最小値を \(\text{dp}_n(x)\) と書くことにします。
\(\text{dp}_n(x)\) は、次の漸化式によって計算できます。
- \(\text{dp}_1(x) = |x| + |x - b_i|\)
- \(\text{dp}_{n+1}(x) = \min_{y\leqq x - a_i}\text{dp}_n(y) + |x| + |x-b_i|\)
しかし、そもそも \(x\) としては無限個の可能性がありますし、すべての \(x\) に対して \(\text{dp}_n(x)\) の値を直接保持することはできません。そこで、\(\text{dp}_n\) と等価な情報を別の形で管理することにします。
◆ 傾きの変化点による関数表現
上述の計算過程で現れる関数 \(\text{dp}_n\) は、傾きが整数であるような \(1\) 次関数をつないでできる凸関数であることが分かります。
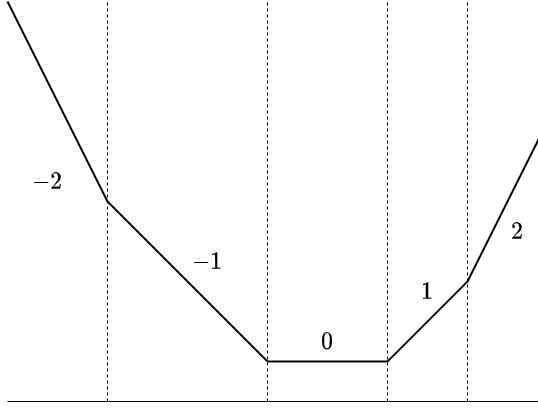
このような関数は、傾きが変化する点の座標集合によって表す ことができ、以下に述べるような関数に対する操作を効率よく行うことができます。
傾きに注目することで区分線形凸関数を上手く取り扱う方法は、「slope trick」などと呼ばれています。以下のような文献を参考にしてください。
- https://maspypy.com/slope-trick-1-%e8%a7%a3%e8%aa%ac%e7%b7%a8 (日本語のみ)
- https://codeforces.com/blog/entry/47821
◆ 本問題で必要な操作
\(\text{dp}_n\) から \(\text{dp}_{n+1}\) を得るために必要な操作を整理しましょう。
\(f = \text{dp}_n\), \(g = \text{dp}_{n+1}\) とします。これらの関係は、\(g(x) = \min_{y\leqq x - a_i}f(y) + |x| + |x-b_i|\) と表されるのでした。\(f\) から \(g\) を得る操作は、次のように分解できます:
- \(f_1(x) = f(x + a_i)\)
- \(f_2(x) = \min_{y\leqq x - a_i}f(y) = \min_{y\leqq x}f(y - a_i) = \min_{y\leqq x}f_1(y)\)
- \(g(x) = f_2(x) + |x| + |x - b_i|\)
つまり、\(g\) は \(f\) から
- 平行移動
- 累積 \(\min\)
- \(|x-a|\) の形の加算
を行うことで得られます。これらは slope trick の基本操作であり、優先度付きキューを用いて効率よく行うことができます。
本問題全体は、\(\Theta(N\log N)\) 時間で解くことができます。
◆ 解答例
posted:
last update: