B - ARC Wrecker 解説 by E869120
この問題は A 問題より難しく、茶色コーダーや緑色コーダーでも苦戦した人が多いのではないかと思います。しかし実装量は非常に軽く、ある考察をすればたったの 300 バイト程度で解くことができるのです。そこで本解説では、
- B 問題「ARC Wrecker」の解法
- どのような考察ステップで解法に至るか
- サンプルコード
の 3 つに分けて紹介します。
1. この問題の解法
\(A = (A_1, A_2, ..., A_N)\) を昇順にソートした配列を \(A' = (A'_1, A'_2, ..., A'_N)\) とします。そのとき、求める通り数は次のようになります。ただし、ここでは \(A'_0 = 0\) とします。
\[ Answer = \prod_{i=1}^{N} \left(A'_i - A'_{i-1} + 1\right) = \left(A'_1 - A'_0 + 1\right) \times \left(A'_2 - A'_1 + 1\right) \times \left(A'_3 - A'_2 + 1\right) \times \cdots \times \left(A'_N - A'_{N-1} + 1\right) \]
これを \(10^{9} + 7\) で割った余りを出力すれば正解となります。なお、\(\prod\) 記号についてはこちらの記事を参照してください。
計算量は、昇順ソートがボトルネックになり、\(O(N \log N)\) となります。例えば C++ では std::sort 関数を使うことで簡単に実装できます。より分かりやすく説明するため、例もいくつか載せておきます。
- \(A = (3, 5, 7)\) のとき:\((3 - 0 + 1) \times (5 - 3 + 1) \times (7 - 5 + 1) = 36\) 通り
- \(A = (31, 41, 59)\) のとき:\((31 - 0 + 1) \times (41 - 31 + 1) \times (59 - 41 + 1) = 6688\) 通り
- \(A = (226, 250, 121)\) のとき:\((121 - 0 + 1) \times (226 - 121 + 1) \times (250 - 226 + 1) = 323300\) 通り
2. どのようにして解法に至るか?
今回のような数え上げ系の問題では、\(N\) が小さい場合を考えると考察が進むことがあります。
- \(N = 1\) の場合
- \(N = 2\) の場合
- \(N = 3\) の場合
- \(N\) が一般の場合
の順序で解説していきましょう。
2-1. \(N = 1\) の場合
ビルは \(1\) 個しかありません。したがって、景観を決める唯一の要素は、
- ビル \(1\)(左から \(1\) 番目のビル)の高さがどうなっているか
となります。これは、大砲の発射回数に応じて \(0\) 階から \(A_1\) 階まであり得るので、求める答えは \(A_1 + 1\) 通りとなります。
2-2. \(N = 2\) の場合
これがかなり本質的です。最初の時点では、
- \(P_1 = min(A_1, A_2)\) 個の「\(2\) つのビルが存在する階」
- \(P_2 = max(A_1, A_2) - min(A_1, A_2)\) 個の「\(1\) つのビルが存在する階」
があります。例えば \(A_1 = 3, A_2 = 5\) の場合、{\(1, 2, 3\)} 階には \(2\) つのビルが存在し、{\(4, 5\)} 階には \(1\) つのビルが存在します。
そこで、\(1\) 回大砲を撃つと、次のうちいずれかがの変化が起こることが分かります。
- 「\(1\) つのビルが存在する階」の個数 \(P_1\) が \(1\) 個減る(\(1\) つのビルがある階に大砲を撃った場合)
- 「\(2\) つのビルが存在する階」の個数 \(P_2\) が \(1\) 個減る(\(2\) つのビルがある階に大砲を撃った場合)
といった感じになります。このように考えると、最終的な \(P_1, P_2\) の値は、
- \(P_1\):\(0\) 個から \(min(A_1, A_2)\) 個までの \(min(A_1, A_2) + 1\) 通りあり得る
- \(P_2\):\(0\) 個から \(max(A_1, A_2) - min(A_1, A_2)\) 個までの \(max(A_1, A_2) - min(A_1, A_2) + 1\) 通りあり得る
ため、求める答えは \(\left(min(A_1, A_2) + 1\right) \times \left(max(A_1, A_2) - min(A_1, A_2) + 1\right)\) 通りとなります。

2-3. \(N = 3\) の場合
「\(1\) つのビルがある階」「\(2\) つのビルがある階」「\(3\) つのビルがある階」がいくつかあると思いますが、\(1\) 階大砲を撃つと次のうちいずれかの変化が起こります。
- 「\(1\) つのビルが存在する階」の個数 \(P_1\) が \(1\) 個減る(\(1\) つのビルがある階に大砲を撃った場合)
- 「\(2\) つのビルが存在する階」の個数 \(P_2\) が \(1\) 個減る(\(2\) つのビルがある階に大砲を撃った場合)
- 「\(3\) つのビルが存在する階」の個数 \(P_3\) が \(1\) 個減る(\(3\) つのビルがある階に大砲を撃った場合)
2-2. 節で記した通り、まだ大砲を一度も撃っていない、最初の時点での \(P_1, P_2, P_3\) の値をそれぞれ \(Q_1, Q_2, Q_3\) とすると、求める答えは \((Q_1 + 1) \times (Q_2 + 1) \times (Q_3 + 1)\) と表されます。そこで、数列 \(A = (A_1, A_2, A_3)\) を昇順にソートしたものを \(A' = (A'_1, A'_2, A'_3)\) とするとき、
- \(Q_1 = A'_1\)
- \(Q_2 = A'_2 - A'_1\)
- \(Q_3 = A'_3 - A'_2\)
と表されるため、答えは \((A'_1 + 1) \times (A'_2 - A'_1 + 1) \times (A'_3 - A'_2 + 1)\) となるのです。例えば \(A = (3, 2, 4)\) の場合、下図のように考えて \(12\) 通りとなります。
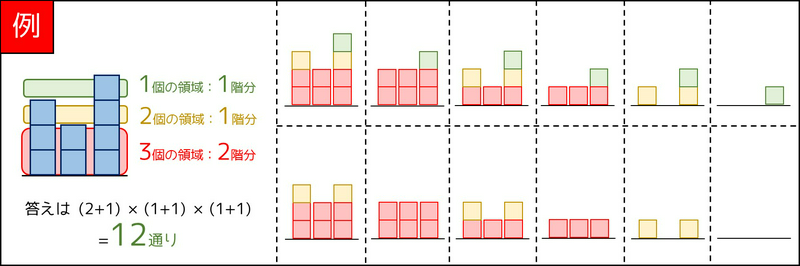
2-4. \(N\) が一般の場合
2-3. 節まで理解したら、ほとんど解法に至っているようなものです。一般に、最初の時点で「ビルが \(i\) 個存在する階」が \(Q_i\) 個あるとすると、最終的な景観において「ビルが \(i\) 個存在する階」は \(0\) 個から \(Q_i\) 個までの \(Q_i + 1\) 通りあり得ます。したがって、求める答えは
\[ (Q_1 + 1) \times (Q_2 - Q_1 + 1) \times (Q_3 - Q_2 + 1) \times \cdots \times (Q_N - Q_{N-1} + 1) \]
となるのです。数列 \(A\) を昇順にソートしたものを \(A' = (A'_1, A'_2, \cdots, A'_N)\) とするとき、\(Q_i = A'_i - A'_{i-1}\) となるため、求める答えは次のようになります。
\[ Answer = \prod_{i=1}^{N} \left(A'_i - A'_{i-1} + 1\right) = \left(A'_1 - A'_0 + 1\right) \times \left(A'_2 - A'_1 + 1\right) \times \left(A'_3 - A'_2 + 1\right) \times \cdots \times \left(A'_N - A'_{N-1} + 1\right) \]
3. サンプルコード
まず、C++ での解答例は次のようになります。(リンク)
#include <iostream>
#include <algorithm>
using namespace std;
#pragma warning (disable: 4996)
long long mod = 1000000007;
long long N, A[1 << 18], Q[1 << 18];
long long Answer = 1;
int main() {
// Input, Sorting
cin >> N;
for (int i = 1; i <= N; i++) cin >> A[i];
sort(A + 1, A + N + 1);
for (int i = 1; i <= N; i++) Q[i] = A[i] - A[i - 1];
// Get Answer
for (int i = 1; i <= N; i++) {
Answer *= (Q[i] + 1LL);
Answer %= mod;
}
cout << Answer << endl;
return 0;
}
他のプログラミング言語でのサンプルコードは、次の通りです。
投稿日時:
最終更新: