F - Gateau Editorial
by  square1001
square1001
本コンテストの最終問題です。
まず、この問題の条件を数式で整理してみましょう。ピース \(i\) \((0 \leqq i \leqq 2N-1)\) の上に載せるいちごの個数を \(b_i\) (\(0\) 以上の整数) とすると、友人 \(i\) の希望は次式で表されます。
- \(i < N\) のとき「\(b_i + b_{i+1} + \cdots + b_{i+N-1} \geqq A_i\)」
- \(i \geqq N\) のとき「\(b_i + b_{i+1} + \cdots + b_{2N-1} + b_0 + \cdots + b_{i-N-1} \geqq A_i\)」
この条件を満たしたうえで、全体のいちごの個数 \(b_0 + b_1 + \cdots + b_{2N-1}\) を最小化するのが、この問題でやりたいことです。
別の言葉でいえば、長さ \(2N\) の円環の半分の区間それぞれについて、合計がいくつ以上になっていなければならない、といった制約がついているときに、全体の合計の最小値がいくつかを求める問題になります。
この解説では、解法のステップを順々に説明していきます。なお、急いで解説を読みたい人は ステップ 5. をお読みください。
ステップ 1. 答えを二分探索する
まず、全体で必要ないちごの個数の最小値を \(X_{opt}\) とします。このとき、以下の重要な性質がなりたっています。
- \(X \geqq X_{opt}\) のとき、全体のいちごの個数をちょうど \(X\) 個にできる
- \(X < X_{opt}\) のとき、全体のいちごの個数をちょうど \(X\) 個にはできない
つまり、この境界となる \(X\) を求めると「最適解 \(X_{opt}\)」になっているのです。これを二分探索によって求めると、元々より簡単な以下の問題に落とし込めるのです。
- 全体のいちごの個数をちょうど \(X\) 個にできるか?
全体の個数が定まると、とても都合の良いことが起こります。なぜなら、”表の区間” の条件を “裏の区間” の条件に置き換えることができるからです。具体的には、以下の \(2\) つの条件が同一のものになります。
- \(b_0 + b_1 + \cdots + b_{l-1} + b_r + \cdots + b_{2N-1} \geqq \alpha\)
- \(b_l + b_{l+1} + \cdots + b_{r-1} \leqq X - \alpha\)
このアイデアを使うと、先ほど扱いづらそうに見えた \(i \geqq N\) の条件を、次のように単純化することができます。
- \(b_{i-N} + b_{i-N+1} + \cdots + b_{i-1} \leqq X - A_i\)
これで、すべてを「長さ \(N\) の区間の条件」に置き換えることができたことになり、少しは解きやすそうな見た目になったと思います。
ステップ 2. 累積和で条件を分かりやすく整理
区間の条件なので、累積和で書き表してみるとさらに単純な式になります。ここで、\(s_i = d_0 + d_1 + \cdots + d_{i-1}\) としましょう。
すると、友人 \(i\) の希望は、次の式で置き換えることができます。
- \(i < N\) のとき「\(s_{i+N} - s_i \geqq A_i\)」
- \(i \geqq N\) のとき「\(s_i - s_{i-N} \leqq X - A_i\)」
つまり、\(L_i = A_i, R_i = X - A_{i+N}\) とすると、以下の条件をすべて成り立たせるのが可能か判定する問題になるのです。
- \(0 = s_0 \leqq s_1 \leqq \cdots \leqq s_{2N} = X\)
- \(i = 0, 1, \dots, N-1\) に対して \(L_i \leqq s_{i+N} - s_i \leqq R_i\)
ステップ 3. 特殊な場合を考えてみる
先ほどの判定問題をどうやって解くのか、方針が見えにくいと思います。そのような時には、特殊なパターンの解法からアイデアを思いつく というテクニックで解法が思いつきやすくなる場合があります。
まずは、全ての \(i\) に対して \(L_i = R_i\) の場合、すなわち \(s_{i+N} - s_i\) の値が最初から定まっている場合を考えてみましょう。この場合、以下のような問題になります。
次の条件を満たす整数の列 \(s_0, s_1, \dots, s_{2N-1}\) は存在するか?
- \(0 = s_0 \leqq s_1 \leqq \cdots \leqq s_{2N-1} \leqq X\)
- \(i = 0, 1, \dots, N-1\) に対して \(s_{i+N} - s_i = D_i\) が成り立つ
(ただし、ここでは \(L_i, R_i\) の値を \(D_i\) とする)
これは、以下のような貪欲法アルゴリズムを使って判定することができます。
- まず \(s_0 = 0, s_N = D_0\) が分かっている
- \(i = 1, 2, \dots, N-1\) の順に、以下の処理を行う
- \(s_{i+N-1} - s_{i-1} \leqq D_i\) ならば、\((s_i, s_{i+N}) = (s_{i-1}, s_{i-1} + D_i)\) とする
- \(s_{i+N-1} - s_{i-1} > D_i\) ならば、\((s_i, s_{i+N}) = (s_{i+N-1} - D_i, s_{i+N-1})\) とする
- 最終的に \(s_{N-1} \leqq s_N\) と \(s_{2N-1} \leqq X\) が両方成り立っていれば、条件を満たすものが作れている。片方でも成り立っていない場合、条件を満たすものは存在しない。
貪欲アルゴリズムの実行例の \(1\) つを図で表すと、以下のようになります。これは \(D = (10, 12, 13, 9, 11, 8, 6)\) の場合です。
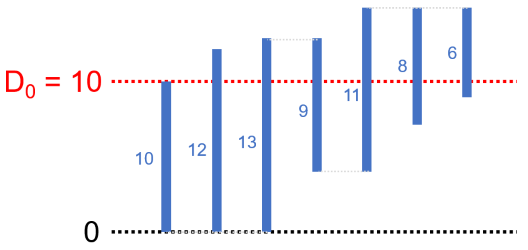
つまり、\((s_0, s_N), (s_1, s_{N+1}), \dots, (s_{N-1}, s_{2N-1})\) の順に、\(s_0 \leqq s_1 \leqq \cdots \leqq s_{2N-1}\) の条件を満たすギリギリのペアを作っていく、というアイデアです。これは以下の理由で最適な構成方法になっています。
- \(s_{N-1}\) と \(s_{2N-1}\) が小さいほど、最終的な条件が成り立ちやすくなる
- 2. の操作では、\(s_i, s_{i+N}\) がともに最小になるものを順に作っている
ステップ 4-1. 一般の場合にも解けないか考える
先ほどは、\(L_i = R_i\) という特殊な条件が成り立っている場合に、比較的直感的なアルゴリズムで解く方法を説明しました。今度は、ステップ 3 のアイデアを応用して、\(L_i \leqq R_i\) である一般の場合に判定問題を解けないか考えてみます。
まず、ステップ 3 のアルゴリズムの手順 3. について「\(s_{N-1} \leqq s_N\) と \(s_{2N-1} \leqq X\) が両方成り立っているかどうかで決まる」とあります。しかし、\(s_N\) の値は、\(L_0 \leqq s_N \leqq R_0\) の値ならば何でもよいことになっています。
ここで、\(s_N\) の値が \(M\) に決まっている場合に解けるか考えてみましょう。実は、ステップ 3 と同様の、\((s_0, s_N), (s_1, s_{N+1}), \dots, (s_{N-1}, s_{2N-1})\) の順に、\(s_0 \leqq s_1 \leqq \cdots \leqq s_{2N-1}\) の条件を満たすギリギリのペアを作っていくというアイデアで、解くことができます。
- まず \(s_0 = 0, s_N = M\) が分かっている
- \(i = 1, 2, \dots, N-1\) の順に、以下の処理を行う
- \(L_i \leqq s_{i+N-1} - s_{i-1} \leqq R_i\) ならば、\((s_i, s_{i+N}) = (s_{i-1}, s_{i+N-1})\) とする
- \(s_{i+N-1} - s_{i-1} < L_i\) ならば、\((s_i, s_{i+N}) = (s_{i-1}, s_{i-1} + L_i)\) とする
- \(s_{i+N-1} - s_{i-1} > R_i\) ならば、\((s_i, s_{i+N}) = (s_{i+N-1} - R_i, s_{i+N-1})\) とする
- 最終的に \(s_{N-1} \leqq s_N\) と \(s_{2N-1} \leqq X\) が両方成り立っていれば、条件を満たすものが作れている。片方でも成り立っていない場合、条件を満たすものは存在しない。
これで一般の場合に解法を拡張できました。しかし、このアルゴリズムは \(s_N\) の値が求まっていなければ通用しません。
もちろん \(s_N\) の値を全探索することもできますが、\(A = \max(A_0, A_1, \dots, A_{2N-1})\) とすると判定問題を解くのに計算量 \(O(NA)\) 掛かってしまい、実行時間制限には当然間に合いません。
ステップ 4-2. \(s_N\) の値を決め打ちしよう
アルゴリズムを効率化するための最大の問題点となっているのは、以下の通りです。
- \(s_N\) の値が決められないせいで、効率的な貪欲法アルゴリズムが作れていないこと
問題を解決するためには、上手く \(s_N\) の値を決める方法を見つける必要が出てきます。どんな \(s_N\) の値ならば、\(s_{2N-1} \leqq X\) が成り立つのか、あるいは \(s_{N-1} \leqq s_N\) が成り立つのかを考えてみましょう。
ここで使うのは以下の重要な性質です。直感的に分かりやすい性質ですが、証明をすることもできます。
\(s_0, s_N\) の値が今以上になったときに、\(s_{N-1}, s_{2N-1}\) の値も今以上になる。
つまり、\(s_0 = a, s_N = b\) として、ステップ 4-1. の貪欲法アルゴリズムで得られる \(s_{N-1}, s_{2N-1}\) の値をそれぞれ \(f_1(a, b), f_2(a, b)\) とするとき、\(a \leqq a', b \leqq b'\) ならば \(f_1(a, b) \leqq f_1(a', b'), f_2(a, b) \leqq f_2(a', b')\) が成り立つ。
条件 \(s_{2N-1} \leqq X\) について
\(s_N\) の値が大きくなるほど \(s_{2N-1}\) の値が大きくなるので、この条件が成り立つのは \(s_N\) が一定値以下のとき(一定値が \(-\infty\) の場合もある)、といえます。
条件 \(s_{N-1} \leqq s_N\) について
\(s_N\) の値が大きくなるほど \(s_N - s_{N-1}\) は小さくなります。なぜなら、仮想的に \(s_0 = -M, s_N = 0\) とおくと、\(M\) の値が小さくなるほど \(s_{N-1}\) の値が大きくなるからです。
よって、この条件が成り立つのは \(s_N\) が一定値以上のとき(一定値が \(\infty\) の場合もある)、となります。
これより、条件を満たす数列が作れるような \(s_N\) の範囲を二分探索で求めることができ、判定問題を \(O(N \log A)\) で解くことができました。
ステップ 5. まとめ
まとめると、以下のような方針で解けます。
- 全体のいちごの個数 \(X\) を二分探索することで、「これが実現可能か」の判定問題に帰着する
- いちごの個数の累積和 \(s_0, s_1, \cdots, s_{2N}\) について、条件は \(L_i \leqq s_{i+N} - s_i \leqq R_i\) の形で表せる
- \(s_N\) の値が決まれば、貪欲法によって判定問題が解ける
- 実現可能な \(s_N\) の値はある \(1\) つの範囲になるので、これを二分探索で求める
- これより、判定問題を \(O(N \log A)\) で解くことができ、全体の計算量は \(O(N \log^2 A)\) となる
全体計算量が \(O(N \log^2 A)\) なので、\(N = 150\,000, A_i \leqq 500\,000\,000\) という制約下では、適切に実装すれば実行時間制限に間に合わせることができます。
なお、判定問題を \(O(N)\) で解く方法も存在し、これができると全体計算量 \(O(N \log A)\) でこの問題を解くことができます。
おまけ:線形計画問題 (LP) との関連性
線形計画問題 (LP) は、以下のような問題です。
「\(a_1 x_1 + a_2 x_2 + \cdots + a_n x_n \leqq b\)」という形式の条件がたくさんあるときに、上手く \((x_1, x_2, \cdots, x_n)\) を決めたときの \(c_1 x_1 + c_2 x_2 + \cdots + c_n x_n\) の最大値を求める。
そもそも条件を満たす\((x_1, x_2, \cdots, x_n)\) がない場合や、答えを無限に大きくできる場合は、そのことを報告する。
線形計画問題の解法として 単体法 や 内点法 が知られていますが、特殊な形の線形計画問題はより単純かつ高速なアルゴリズムで解けることが知られています。
この一つの例が「差分制約系」です。差分制約系は、以下のような形式の問題です。
- \(x_1, x_2, \dots, x_n\) を実数とする
- 条件は「\(x_{v_1} - x_{u_1} \leqq d_1, x_{v_2} - x_{u_2} \leqq d_2, \cdots, x_{v_m} - x_{u_m} \leqq d_m\) がすべて成り立つこと」
- 条件を満たす \(x_1, x_2, \dots, x_n\) の組み合わせの中で、\(x_t - x_s\) の最大値を求めたい
つまり、「\(2\) つの値の差がいくつ以下」という条件がたくさんあったときに \(x_t - x_s\) を最大化する問題、ということです。
実は、この問題は最短路問題として解くことができるのです。
\(n\) 頂点 \(m\) 辺のグラフを構築し、\(i\) 番目の辺を \(u_i \rightarrow v_i\) に向かう重み \(d_i\) の辺とします。このとき、\(x_t - x_s\) の最大値は、頂点 \(s\) から \(t\) に向かう最短経路の長さと同じになるのです。
本問題においても、ステップ 2. で得られた問題は、\(s_0, s_1, \cdots, s_{2N-1}\) に対する差分制約系の線形計画問題になっています。ですので、ベルマン・フォード法 を用いて判定問題を \(O(N^2)\) で解くことができ、全体計算量は \(O(N^2 \log A)\) となります。(実行時間制限には間に合いません)
しかし、本問題で作られるグラフは特殊な形をしているので、工夫すると \(O(N)\) で最短経路長を求めることができます。これをベースにして、全体計算量 \(O(N \log A)\) で解く方法もあります。
サンプルコード
各言語における解答例は、次の通りです。
posted:
last update: