 /
/ 
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 500 点
問題文
2 つの整数 A, B が与えられます。
各マスが白または黒に塗られたグリッドであって以下の条件を満たすものを、出力の項で指定されたフォーマットに従って一つ出力してください。
- グリッドの大きさを縦 h 行横 w 列としたとき、h および w はともに 100 以下である。
- 白く塗られたマスの集合はちょうど A 個の連結成分に分かれている (連結成分という単語の定義については後の注釈を参照)。
- 黒く塗られたマスの集合はちょうど B 個の連結成分に分かれている。
制約の項で指定される条件のもとで解は必ず一つ以上存在することが証明できます。 解が複数ある場合、どれを出力しても構いません。
注釈
2 つの白く塗られたマス c_1, c_2が連結であるとは、マス c_1 からマス c_2 へ、上下左右に隣り合うマスへの移動を繰り返して、 白く塗られたマスだけを通って移動できることを意味します。
白く塗られたマスの集合 S が連結成分であるとは、S が以下の条件を満たすことを意味します。
- S のどの 2 つのマスも連結である。
- S に含まれないどの白く塗られたマスと、S に含まれるどのマスも連結ではない。
黒く塗られたマスについても連結成分を同様に定義します。
制約
- 1 \leq A \leq 500
- 1 \leq B \leq 500
入力
入力は以下の形式で標準入力から与えられる。
A B
出力
以下の形式で出力せよ。
- 1 行目には構成したグリッドの大きさを表す整数 h, w を空白を区切りとして出力せよ。
- 続いて h 行出力せよ。このうちの i 行目 (1 \leq i \leq h) には以下のような長さ w の文字列 s_i を出力せよ。
- 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが白く塗られているならば、s_i の j 文字目は
.である。 - 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが黒く塗られているならば、s_i の j 文字目は
#である。
- 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが白く塗られているならば、s_i の j 文字目は
入力例 1
2 3
出力例 1
3 3 ##. ..# #.#
この出力は以下のグリッドに対応します。
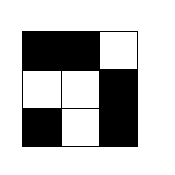
入力例 2
7 8
出力例 2
3 5 #.#.# .#.#. #.#.#
入力例 3
1 1
出力例 3
4 2 .. #. ## ##
入力例 4
3 14
出力例 4
8 18 .................. .................. ....##.......####. ....#.#.....#..... ...#...#....#..... ..#.###.#...#..... .#.......#..#..... #.........#..####.
Score : 500 points
Problem Statement
You are given two integers A and B.
Print a grid where each square is painted white or black that satisfies the following conditions, in the format specified in Output section:
- Let the size of the grid be h \times w (h vertical, w horizontal). Both h and w are at most 100.
- The set of the squares painted white is divided into exactly A connected components.
- The set of the squares painted black is divided into exactly B connected components.
It can be proved that there always exist one or more solutions under the conditions specified in Constraints section. If there are multiple solutions, any of them may be printed.
Notes
Two squares painted white, c_1 and c_2, are called connected when the square c_2 can be reached from the square c_1 passing only white squares by repeatedly moving up, down, left or right to an adjacent square.
A set of squares painted white, S, forms a connected component when the following conditions are met:
- Any two squares in S are connected.
- No pair of a square painted white that is not included in S and a square included in S is connected.
A connected component of squares painted black is defined similarly.
Constraints
- 1 \leq A \leq 500
- 1 \leq B \leq 500
Input
Input is given from Standard Input in the following format:
A B
Output
Output should be in the following format:
- In the first line, print integers h and w representing the size of the grid you constructed, with a space in between.
- Then, print h more lines. The i-th (1 \leq i \leq h) of these lines should contain a string s_i as follows:
- If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted white, the j-th character in s_i should be
.. - If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted black, the j-th character in s_i should be
#.
- If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted white, the j-th character in s_i should be
Sample Input 1
2 3
Sample Output 1
3 3 ##. ..# #.#
This output corresponds to the grid below:

Sample Input 2
7 8
Sample Output 2
3 5 #.#.# .#.#. #.#.#
Sample Input 3
1 1
Sample Output 3
4 2 .. #. ## ##
Sample Input 4
3 14
Sample Output 4
8 18 .................. .................. ....##.......####. ....#.#.....#..... ...#...#....#..... ..#.###.#...#..... .#.......#..#..... #.........#..####.