 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋くん様は、アットコーダー王国の王様です。彼が統治するアットコーダー王国は、1 から N までの番号が付けられた N 個の都市とそれらを結ぶ双方向に行き来可能な M 本の道路からなります。それぞれの道路には長さがあります。 アットコーダー王国の任意の都市の組み合わせ (A,B) について、A からいくつかの道路を辿って B に辿り着けることが保障されています。
高橋くん様は、アットコーダー国民の幸せが、交通の利便性に大きく依存していると考えています。 国民がどれくらい幸せかを調べるために、ありうる全ての都市間の最短経路長の総和 S を求めたいと思っています。
都市 i と j の間の最短経路長を D(i,j) とすれば S は、
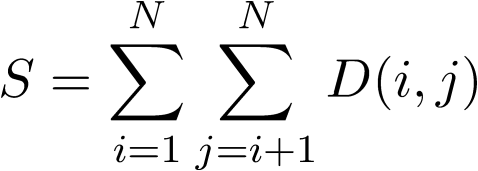
と表されます。
また、高橋くん様は公共事業で、K 本の新たな道路を建設しようと思っています。 この建設によって、ある都市間を直接結ぶ道路が 2 本以上存在してしまうことがありますが、その場合、既にある道路は取り壊さず、新しく追加します。
あなたの仕事は、新たな道路を与えられた順番に建設していき、建設の度に前述の S を計算するプログラムを書くことです。
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 A_2 B_2 C_2 : A_M B_M C_M K X_1 Y_1 Z_1 : X_K Y_K Z_K
- 1 行目には、都市の数と道路の数を表す 2 つの整数 N (1 ≦ N ≦ 400) と M (1 ≦M ≦ 1000) がスペース区切りで与えられる.
- 2 行目からの M 行には、既存の道路の情報が与えられる。そのうち i (1≦i≦M) 行目には、i 番目の道路の情報を表す 3 つの整数 A_i(1≦A_i≦N)、 B_i(1≦B_i≦N)、 C_i(1≦C_i≦1,000) がスペース区切りで与えられる。これは、i 番目の道路が都市 A_i と B_i を距離 C_iで結んでいることを表す。A_i≠B_i であり、同じ都市間を直接結ぶ道路は高々 1 つである。
- 任意の都市の組み合わせ (A,B) について、A からいくつかの道路を辿って B に辿り着けることが保障されている。
- 2+M 行目には、新たに建設する道路の数を表す K (1≦K≦400) が書かれている。
- 3+M 行目からの K 行には、新たに建設する道路の情報が与えられる。そのうち i (1≦i≦K) 行目には、i 番目の新たな道路の情報を表す 3 つの整数 X_i(1≦X_i≦N)、 Y_i(1≦Y_i≦N)、 Z_i(1≦Z_i≦1,000) がスペース区切りで与えられる。i 番目の新たな道路が都市 X_i と Y_i を距離 Z_i で結ぶことを表す。X_i≠Y_i である。
出力
出力は以下の形式で標準出力に行うこと。
i (1≦i≦K) 行目には、i 番目までの新たな道路を建設した直後の、ありうる全ての都市間の最短経路長の総和 S を出力せよ。
末尾の改行を忘れないこと。
入力例1
4 3 1 2 1 2 3 1 3 4 10 2 3 4 1 1 4 1
出力例1
10 8
初期状態は以下の通りです。
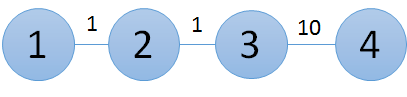
一度目の建設の直後、グラフは以下のようになります。
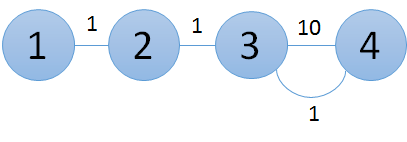
二度目の建設の直後、グラフは以下のようになります。
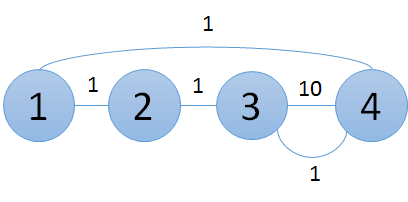
入力例2
8 16 8 7 38 2 8 142 5 2 722 8 6 779 4 6 820 1 3 316 1 7 417 8 3 41 1 4 801 3 2 126 4 2 71 8 4 738 4 3 336 7 5 717 5 6 316 2 1 501 10 6 1 950 6 1 493 1 6 308 3 4 298 2 5 518 1 5 402 4 7 625 7 6 124 3 8 166 2 4 708
出力例2
13649 12878 11954 11954 11280 11058 11058 8099 8099 8099