 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
n 個の頂点と m 本の辺から成る有向グラフがあります.n 個の頂点は, 1 から n の相異なる整数で番号付けされています.
各頂点には,a から z のアルファベットが 1 つ書かれています.
あなたはこのグラフを好きな頂点から開始し,各頂点を任意の順番で訪問することで,ちょうど k 個のアルファベットを回収したいです. 頂点は何度も訪問することができ,その頂点にアルファベットが存在する場合は任意の訪問タイミングで回収することが出来ますが,アルファベットは一度回収すると無くなります.必要がなければ,回収しなくても良いです.
あなたは,ただ回収するだけでは退屈であると思ったので,それらの k 個のアルファベットを回収した順番に並べたときに辞書順最小になるように回収することにしました.
そのような回収方法を行ったときの,k 個のアルファベットを,回収した順番に出力しなさい. k 個のアルファベットを回収する方法が存在しない場合は,-1 を出力しなさい.
入力
入力は以下の形式で標準入力から与えられる.
n m k
c_1 c_2 … c_n
a_1 b_1
a_2 b_2
:
a_{m} b_{m}
- 1 行目には,グラフの頂点の数を表す整数 n (1 ≦ n ≦ 300) と 辺の数を表す整数 m (0 ≦ m ≦ 1000) と回収したいアルファベットの数を表す整数 k (1≦k≦n) が与えられる.
- 2 行目には,頂点 i に書かれているアルファベット c_i(
aからzの小文字アルファベット) が n 個,スペース区切りで与えられる. - 3 行から m 行,グラフの i 番目の有向辺が繋いでいる頂点の番号 a_i と b_i (1≦a_i,b_i≦n) が与えられる. これは,i 番目の辺が,a_i から b_i に移動できる有向辺であることを表す.
- 与えられるグラフに自己辺や多重辺は存在しないが,逆辺は存在することがある.また,連結であることは保障されていない.
出力
1 行目に,辞書順最小となるように回収した k 個のアルファベットを,回収した順番に出力せよ.k 個のアルファベットを回収する方法が存在しない場合は,-1 を出力せよ.最後に改行を忘れないこと.
入力例1
4 4 3 a b b a 1 2 2 3 3 1 4 3
出力例1
aab
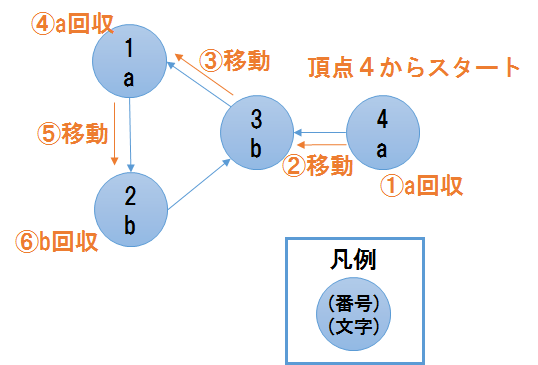
この入出力例を説明する図は以下の通りとなります.頂点 4 → 3 → 1 → 2 と移動する過程で,頂点 4 の a,頂点 1 の a,そして頂点 2 の b を順番に回収することで辞書順最小の答えとなります.
入力例2
5 4 4 d a b c a 1 2 2 3 3 4 2 5
出力例2
dabc
入力例3
5 4 3 d a b c a 1 2 2 3 3 4 2 5
出力例3
abc
入力例4
3 0 2 a b c
出力例4
-1
3 つの頂点は孤立しており,どの頂点から開始しても,ちょうど 2 個のアルファベットを回収することはできません.