C - 暗闇帰り道
解説
 /
/ 
高橋君は、夜道を通って学校から自宅へと 1 人で帰ろうとしています。
彼の住む街は長方形の形をしており、格子状の区画に区切られています。彼は東西南北に 1 秒に 1 区画ずつ移動することができます。
各区画には日当たりの良さが与えられ、経過時間 t 秒(出発時間は 0 秒)を用いて「“各区画の明るさ” = 日当たりの良さ × 0.99^t」と表すことが出来ます。
学校から自宅まで帰る途中に通る経路上の区画における“区画の明るさ”の最小値を、その経路における“経路の明るさ”とします。
高橋君は暗所恐怖症なので、“経路の明るさ”がなるべく大きい経路を選択したいと考えています。
そのような経路を選択した場合の、“経路の明るさ”を求めなさい。
入力は以下の形式で与えられる。
“経路の明るさ”の最大値を標準出力に 1 行で出力せよ。
学校から自宅に帰る経路が存在しない場合は
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 1e−9 以下であれば許容する。
なお、最後には改行を出力せよ。
 /
/ 
実行時間制限: 5 sec / メモリ制限: 64 MiB
問題文
彼の住む街は長方形の形をしており、格子状の区画に区切られています。彼は東西南北に 1 秒に 1 区画ずつ移動することができます。
各区画には日当たりの良さが与えられ、経過時間 t 秒(出発時間は 0 秒)を用いて「“各区画の明るさ” = 日当たりの良さ × 0.99^t」と表すことが出来ます。
学校から自宅まで帰る途中に通る経路上の区画における“区画の明るさ”の最小値を、その経路における“経路の明るさ”とします。
高橋君は暗所恐怖症なので、“経路の明るさ”がなるべく大きい経路を選択したいと考えています。
そのような経路を選択した場合の、“経路の明るさ”を求めなさい。
入力
N M
c_{11}c_{12}…c_{1M}
c_{21}c_{22}…c_{2M}
:
:
c_{N1}c_{N2}…c_{NM}
- 1 行目は、街の南北の長さとして整数 N(1≦N≦500) と東西の長さとして整数 M(1≦M≦500) が空白で区切られて与えられる。
- 2 行目から N 行は、格子状の街の各区画における状態 c_{ij} がそれぞれ
s,g,1-9,#のいずれかで与えられる。 - i+1 行目 j 文字目の文字 c_{ij} は、座標 (j,i) が下記のような状態であることを表す。
s: その区画が学校であることを表す。g: その区画が自宅であることを表す。1-9: その区画の日当たりの良さを表す。#: その区画に侵入出来ないことを表す。
- 与えられた街の外を通ることは出来ない。
sとgはそれぞれ 1 つずつ与えられ、sとgは隣接していない。
出力
学校から自宅に帰る経路が存在しない場合は
-1 と 1 行で出力せよ。誤差は絶対誤差あるいは相対誤差の少なくとも片方が 1e−9 以下であれば許容する。
なお、最後には改行を出力せよ。
入力例 1
3 3 s52 743 32g
出力例 1
2.910897
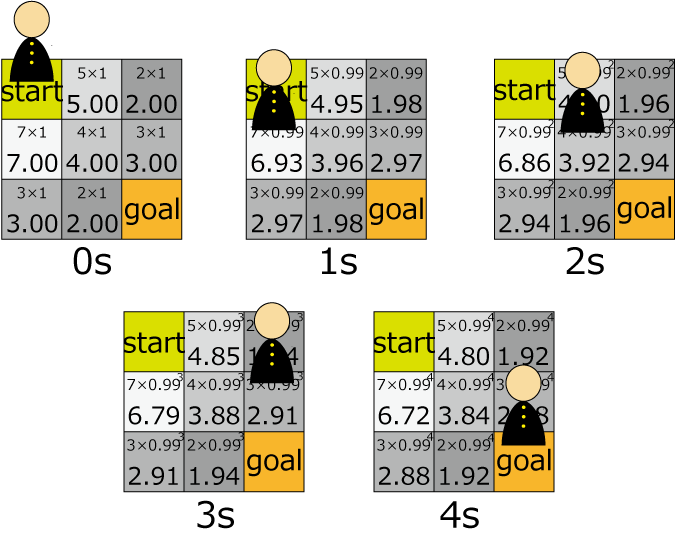
- 時刻0: 学校 (1,1) を出発します。
- 時刻1: (2,1) に移動します。時刻 t=1, 日当たりの良さ=7 なので、(2,1) の明るさは 6.93 です。
- 時刻2: (2,2) に移動します。時刻 t=2, 日当たりの良さ=4 なので、(2,2) 明るさは 3.9204 です。
- 時刻3: (2,3) に移動します。時刻 t=3, 日当たりの良さ=3 なので、(2,3) 明るさは 2.910897 です。
- 時刻4: 自宅 (3,3) に移動します。ここまで一番暗かったのは、時刻 t=3 の (2,3) における明るさ 2.910897 なので、答えは 2.910897 となります。
入力例 2
4 6 g31784 621415 627914 7451s3
出力例 2
2.97
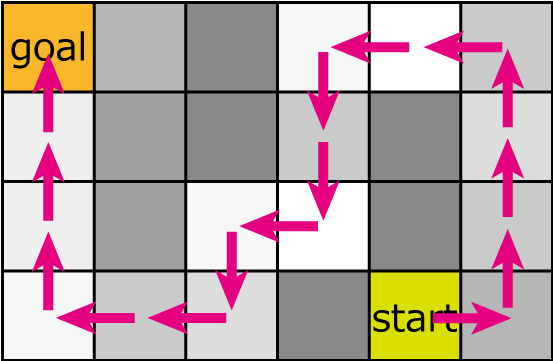
- 下記のようなルートを通る時、明るさが 2.97 となり、これが最善となります。
