A - うるう年
高橋君は忘れっぽい性格なので、うるう年は 2 月 29 日の存在を毎回忘れてしまいます。
そこで、自動でうるう年かどうかをコンピュータに教えてもらえるようにしたいと思います。
入力として与えられた年がうるう年かそうでないかを判断しなさい。
ただし、うるう年は以下の規則で決定します。
2100 年は規則 2 を満たしますが、規則 3 を満たさないのでうるう年ではありません。
入力は以下の形式で標準入力から与えられる。
与えられた年がうるう年ならば
なお、最後には改行を出力せよ。
実行時間制限: 2 sec / メモリ制限: 64 MiB
問題文
そこで、自動でうるう年かどうかをコンピュータに教えてもらえるようにしたいと思います。
入力として与えられた年がうるう年かそうでないかを判断しなさい。
ただし、うるう年は以下の規則で決定します。
- 規則 1:4 で割り切れる年はうるう年である。
- 規則 2:100 で割り切れる年をうるう年ではない。
- 規則 3:400 で割り切れる年はうるう年である。
- 規則 4:規則 1〜3 のいずれも満たさない場合は,うるう年ではありません。
2100 年は規則 2 を満たしますが、規則 3 を満たさないのでうるう年ではありません。
入力
Y
- 年を表す整数 Y(1000 ≦ Y ≦ 2999) が 1 行で与えられる。
出力
YES、そうでなければ NO を標準出力に 1 行で出力せよ。なお、最後には改行を出力せよ。
入力例 1
1001
出力例 1
NO
- 1001 を 4 で割ると 250 あまり 1 になり、規則 1 を満たさないので、うるう年ではありません。
入力例 2
2012
出力例 2
YES
- 2012 を 4 で割ると 503 になり割り切れるので規則 1 を満たします。
- しかし、100では割り切れないので規則 2 は満たさず、うるう年になります(うるう年ではありません、は間違いですので訂正させて頂きました)。
入力例 3
2100
出力例 3
NO
- 2100 は 4 で割り切れるので、規則 1 を満たします。
- また、100 で割ると 21になり割り切れるので、規則 2 を満たします。
- しかし、400 では割り切れず規則 3 を満たさないので、うるう年ではありません。
入力例 4
2000
出力例 4
YES
- 2000 は 4 で割り切れるので、規則 1 を満たします。
- また、100 でも 400 でも割り切れるので規則 2 も 3 も満たします。
- よって、2000 年はうるう年になります。
出典
ARC 002
B - 割り切れる日付
高橋君は割り切れる日付が好きです。
割り切れる日付とは、年÷月÷日の計算結果が整数になる日付のことです。
例えば今日の日付は 2012 年 5 月 2 日ですが、 2012÷5÷2=201.2 となり整数ではないので、今日の日付は割り切れる日付ではありません。
高橋君は割り切れる日付が好きでたまらないので、次の割り切れる日付を心待ちにして、毎日今日が割り切れる日付かどうかをチェックしてしまいます。
彼に少しでも多くの仕事をしてもらうために、入力として与えられた日付以降で最初に来る割り切れる日付を求めなさい。
ただし、入力として与えられた日付が割り切れる日付だった場合は、与えられた日付が答えになります。
入力は以下の形式で標準入力から与えられる。
入力として与えられた日付以降で最初に割り切れる日付を、入力と同じ形式で標準出力に 1 行で出力せよ。
ただし、入力として与えられた日付が割り切れる日付だった場合は、入力と同じ日付を出力すること。
なお、最後には改行を出力せよ。
実行時間制限: 2 sec / メモリ制限: 64 MiB
問題文
割り切れる日付とは、年÷月÷日の計算結果が整数になる日付のことです。
例えば今日の日付は 2012 年 5 月 2 日ですが、 2012÷5÷2=201.2 となり整数ではないので、今日の日付は割り切れる日付ではありません。
高橋君は割り切れる日付が好きでたまらないので、次の割り切れる日付を心待ちにして、毎日今日が割り切れる日付かどうかをチェックしてしまいます。
彼に少しでも多くの仕事をしてもらうために、入力として与えられた日付以降で最初に来る割り切れる日付を求めなさい。
ただし、入力として与えられた日付が割り切れる日付だった場合は、与えられた日付が答えになります。
入力
Y/M/D
- グレゴリオ暦(現在、日本で一般的に使われている暦)に従って年を表す Y、月を表す M、日を表す D が
/で区切られて 1 行で与えられる。 - Y は 4 桁、M と D は 0 埋めされた 2 桁の整数である(M と D は、1 桁の数の場合も 1 桁目に
0をつけて 2 桁にする)。 - 与えられる日付は 1000/01/01 以降、2999/12/31 以前とする。
出力
ただし、入力として与えられた日付が割り切れる日付だった場合は、入力と同じ日付を出力すること。
なお、最後には改行を出力せよ。
入力例 1
2012/05/02
出力例 1
2013/01/01
- 2012/05/02 は割り切れる日付ではないので、2012/05/03 から 2012/12/31 の間の日付に割り切れる日付はないので 2013/01/01 が答えとなります。
入力例 2
2020/05/02
出力例 2
2020/05/02
- 入力として与えられた日付は割り切れる日付なので、2020/05/02 が答えとなります。
入力例 3
2088/02/28
出力例 3
2088/02/29
- 2088 年はうるう年なので、2 月 29 日が存在します。
出典
ARC 002
C - コマンド入力
高橋君は友達と格闘ゲームで対戦をすることにしました。
格闘ゲームは A, B, X, Y の 4 種類のボタンを連続で入力するコマンドにより技を繰り出し戦うゲームです。
しかし、普段格闘ゲームで遊ばない高橋君にとってコマンドの入力は難しく、友達に勝てそうにありません。
そこで余っている L と R のボタンに連続した 2 つのボタン入力をショートカットとして割り当てることで、コマンドの入力を短縮したいと思います。
例えば、コマンドが ABXY だと 4 回ボタンを入力する必要がありますが、L に AB、R に XY を割り当てることで LR の 2 回のボタン入力に短縮できます。
L と R を用いて入力をなるべく短くした時に必要なボタンの入力回数を求めなさい。
入力は以下の形式で標準入力から与えられる。
ショートカットを用いてコマンド入力に必要なボタンの入力回数を最小化したときの、ボタン入力回数を標準出力に 1 行で出力せよ。
なお、最後には改行を出力せよ。
実行時間制限: 2 sec / メモリ制限: 64 MiB
問題文
格闘ゲームは A, B, X, Y の 4 種類のボタンを連続で入力するコマンドにより技を繰り出し戦うゲームです。
しかし、普段格闘ゲームで遊ばない高橋君にとってコマンドの入力は難しく、友達に勝てそうにありません。
そこで余っている L と R のボタンに連続した 2 つのボタン入力をショートカットとして割り当てることで、コマンドの入力を短縮したいと思います。
例えば、コマンドが ABXY だと 4 回ボタンを入力する必要がありますが、L に AB、R に XY を割り当てることで LR の 2 回のボタン入力に短縮できます。
L と R を用いて入力をなるべく短くした時に必要なボタンの入力回数を求めなさい。
入力
N
c_{1}c_{2}...c_{N}
- 1 行目にコマンドに必要なボタンの入力回数を表す N(1 ≦ N ≦ 1000)が与えられる。
- 2 行目にコマンドの内容を表す N 文字の文字列が与えられる。
- i 文字目の文字である c_{i} は、
A,B,X,Yのいずれかで与えられる。
出力
なお、最後には改行を出力せよ。
入力例 1
4 ABXY
出力例 1
2
- L に AB、R に XY を割り当てることで入力を LR に短縮することができ、ボタンの入力回数は 2 回となります。
入力例 2
13 ABABABABXBXBX
出力例 2
7
- L に AB、R に BX を割り当てることで入力を LLLARRR に短縮することができ、ボタンの入力回数は 7 回となります。
入力例 3
8 AABBAABB
出力例 3
4
- L に AA、R に BB を割り当てることで入力を LRLR に短縮することができ、ボタンの入力回数は 4 回となります。
出典
ARC 002
D - ボードゲーム
高橋君は格闘ゲームで友達に負けたのが悔しくてたまらなかったので、今度は自分が勝てるゲームを提案しました。
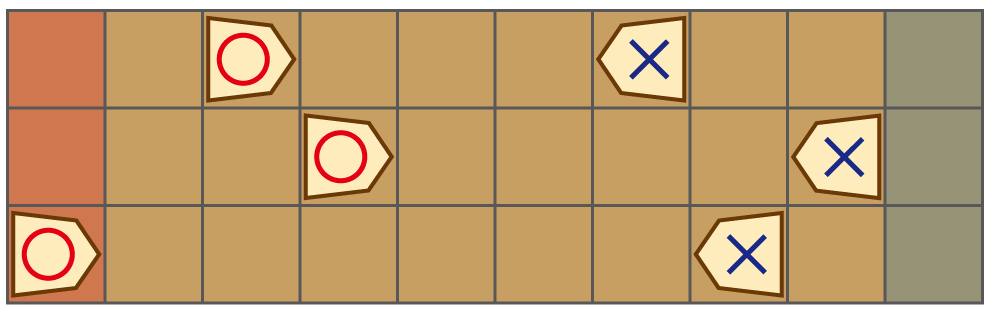
提案するゲームは格子状のマスでできた盤に向かい合って座り、図の左端 1 列が○の陣地、右端 1 列が×の陣地になります。
ランダムに並べられた○と×の駒を用い、2 人はそれぞれ○か×のどちらかを自分の手駒とします。
 駒は相手の陣地に向かって1 マスずつ前進し、相手に踏まれた駒は盤から取り除きます。
駒は相手の陣地に向かって1 マスずつ前進し、相手に踏まれた駒は盤から取り除きます。
前 1方向にのみ進むことができ、それ以外の斜め・横・後ろには進むことができません。
また、自分の駒を踏むことはできません。
交互に 1 つずつ自分の駒を動かし、相手の駒を全て取り除くか、相手の陣地に自分の駒を 1 つでも置いたら勝利となります。
先行は○のついた駒を持っている人ですが、最初の 1 手目では×を取ることのできない初期配置になっています。
また、初期配置で既にどちらかの勝利条件を満たしていることもありません。
高橋君は必ず勝ちたいので○と×のどちらを手駒にするか悩んでいます。
高橋君が勝てるように、○と×のどちらが勝つか判定しなさい。
入力は以下の形式で標準入力から与えられる。
○が勝つ場合は
なお、最後には改行を出力せよ。
実行時間制限: 2 sec / メモリ制限: 256 MiB
問題文
提案するゲームは格子状のマスでできた盤に向かい合って座り、図の左端 1 列が○の陣地、右端 1 列が×の陣地になります。
ランダムに並べられた○と×の駒を用い、2 人はそれぞれ○か×のどちらかを自分の手駒とします。

図:盤面の例。左端の赤い列が○の陣地,右端の青い列が×の陣地となる。
前 1方向にのみ進むことができ、それ以外の斜め・横・後ろには進むことができません。
また、自分の駒を踏むことはできません。
交互に 1 つずつ自分の駒を動かし、相手の駒を全て取り除くか、相手の陣地に自分の駒を 1 つでも置いたら勝利となります。
先行は○のついた駒を持っている人ですが、最初の 1 手目では×を取ることのできない初期配置になっています。
また、初期配置で既にどちらかの勝利条件を満たしていることもありません。
高橋君は必ず勝ちたいので○と×のどちらを手駒にするか悩んでいます。
高橋君が勝てるように、○と×のどちらが勝つか判定しなさい。
入力
H W
c_{11}c_{12}…c_{1W}
c_{21}c_{22}…c_{2W}
:
:
c_{H1}c_{H2}…c_{HW}
- 1 行目には、盤の高さを表す整数 H (1 ≦ H ≦ 2,000)、盤の幅を表す整数 W (3 ≦ W ≦ 2,000) が空白を区切りとして与えられる。
- 2 行目から H 行は、盤の上の駒の配置として各行 W 文字の文字列が与えられる。
- i 行目の先頭から j 番目の文字である c_{ij}は、
.,o,xのいずれかで与えらる。 - c_{ij} が
.の場合は何も駒が置かれていないことを、oは○の駒が、xは×の駒が置かれていることを表す。
出力
oを、×が勝つ場合はx を標準出力に 1 行で出力せよ。なお、最後には改行を出力せよ。
入力例 1
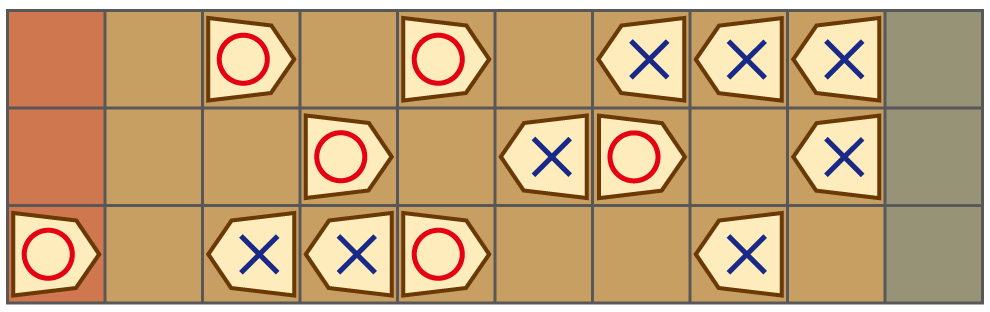
3 10 ..o.o.xxx. ...o.xo.x. o.xxo..x..
出力例 1
o

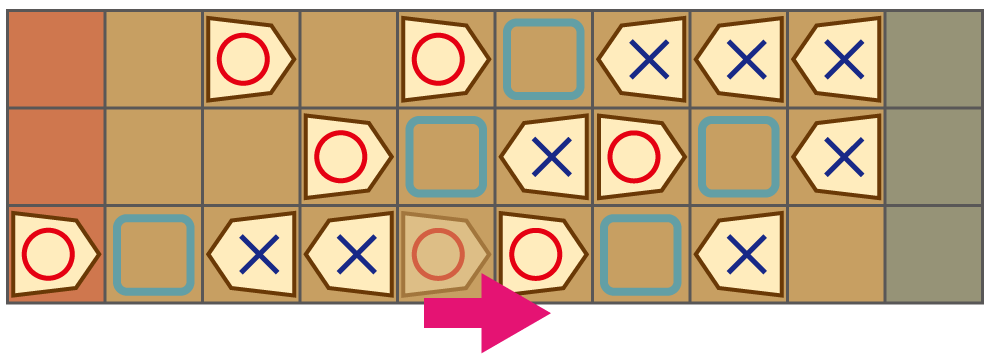
- まず先行の○は 3 段目左から 5 番目の駒を右に進めます。

- ×の番になりましたが、動かせる駒のうちどの駒を左に進めても、次の○の番に駒を取られてしまいます。
- 取られた後も先程同様、どの駒を動かしても次の○の番に進めた駒を取られてしまいます(図の水色枠にしか移動できない)。
- つまり、最初の 1 手目で 3 段目左から 5 番目の駒を右に進めることで、○の勝利が決定します。
入力例 2
3 5 ..x.. .o... ...x.
出力例 2
x
- お互い踏み合うことはなく、○は最短で 3 手、×は 2 手で相手の陣地に到達できるので×の勝利になります。