 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
あなたはA社を経営する社長です。 A社はN個の組織からなり、それぞれに0番からN - 1番の番号が付いています。 0番の番号が付いた組織はトップの組織です。
組織間には親子関係があり、0番以外のN - 1個の組織には必ず1つの親組織があります。 子組織は複数になることがあります。 また、それぞれの組織は直接的または間接的にトップの組織と関係があるものとします。
あなたは全ての組織に報告書を提出するように求めました。 混雑を避けるために、「各組織は子組織の報告書がそろったら、自身の報告書を加えて親組織に渡す」ことを繰り返します。 子組織が無いような組織はすぐに親組織に報告書を渡します。 トップの組織は子組織の報告書がそろったら、自身の報告書を加えて社長に提出します。
それぞれの組織が1枚の報告書を提出します。
各組織について、「その組織が親組織に提出することになる報告書の枚数」を出力するプログラムを作成してください。 ただしトップの組織については「社長に提出する報告書の枚数」を出力してください。
サンプルプログラム
#include <bits/stdc++.h>
using namespace std;
// x番の組織が親組織に提出する枚数を返す
// childrenは組織の関係を表す2次元配列(参照渡し)
int count_report_num(vector<vector<int>> &children, int x) {
// (ここに追記して再帰関数を実装する)
}
// これ以降の行は変更しなくてよい
int main() {
int N;
cin >> N;
vector<int> p(N); // 各組織の親組織を示す配列
p.at(0) = -1; // 0番組織の親組織は存在しないので-1を入れておく
for (int i = 1; i < N; i++) {
cin >> p.at(i);
}
// 組織の関係から2次元配列を作る
vector<vector<int>> children(N); // ある組織の子組織の番号一覧
for (int i = 1; i < N; i++) {
int parent = p.at(i); // i番の親組織の番号
children.at(parent).push_back(i); // parentの子組織一覧にi番を追加
}
// 各組織について、答えを出力
for (int i = 0; i < N; i++) {
cout << count_report_num(children, i) << endl;
}
}
関数count_report_numの引数childrenは二次元配列で、
x番の組織の子組織の番号一覧の配列はchildren.at(x)とすることで得ることができます。
制約
- 1 \leq N \leq 50
- 0 \leq p_i < i (1 \leq i \leq N - 1)
入力
入力は次の形式で標準入力から与えられます。
N
p_1 p_2 p_3 \ldots p_{N - 1}
p_iはi番の組織の親組織がp_i番の組織であることを示します。
0番の組織はトップの組織であり、親組織が存在しないことに注意してください。
出力
ans_0
ans_1
ans_2
\vdots
ans_{N - 1}
0番の組織から順に、i番の組織についての答えans_iを1行毎に出力してください。
ジャッジでは以下の入力例以外のケースに関してもテストされることに注意。
入力例1
6 0 0 1 1 4
出力例1
6 4 1 1 2 1
組織の関係は次の図のようになります。(子組織から親組織の向きに矢印が向いています。)
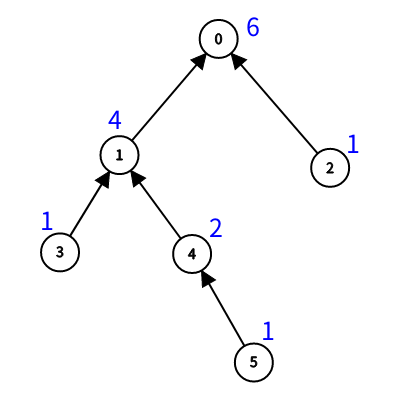
番号の隣に書いてある青い数字が各組織についての答えです。
入力例2
8 0 0 1 2 0 3 6
出力例2
8 4 2 3 1 1 2 1
組織の関係は次の図のようになります。(子組織から親組織の向きに矢印が向いています。)
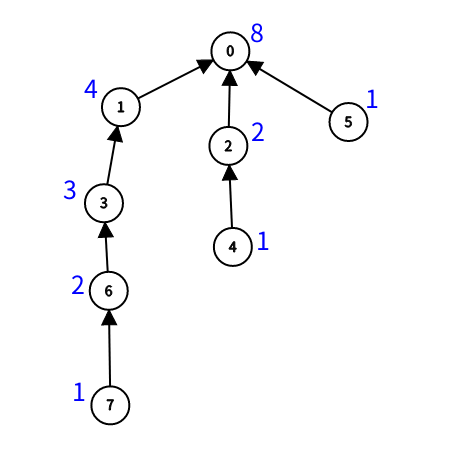
番号の隣に書いてある青い数字が各組織についての答えです。
ヒント
クリックでヒントを開く
- 「組織xが親組織へ提出する枚数」= 組織xの全ての子組織cについて「cから受け取った報告書の枚数」の合計 + 1
- 「cから受け取った報告書の枚数」=「cが親組織に提出する枚数」
- 子組織が無いような組織について、その組織が親組織に提出する報告書の枚数は1枚
次のようにすることでx番の組織の子組織についての処理が行えます。
for (int c : children.at(x)) {
// (cについての処理)
}
この問題は2.05.再帰関数の例題に非常に近い問題となっているので、そちらも参考にしてください。
テスト入出力
書いたプログラムがACにならず、原因がどうしてもわからないときだけ見てください。
クリックでテスト入出力を見る
テスト入力1
20 0 1 1 3 0 0 1 3 5 9 6 8 8 8 0 4 7 12 13
テスト出力1
20 13 1 9 2 3 2 2 6 2 1 1 2 2 1 1 1 1 1 1
テスト入力2
30 0 1 0 1 0 3 1 2 8 6 1 3 0 4 2 3 0 14 16 13 5 2 16 14 19 2 7 2 26
テスト出力2
30 16 8 8 4 2 2 2 2 1 1 1 1 2 3 1 4 1 1 2 1 1 1 1 1 1 2 1 1 1
テスト入力3
50 0 0 0 2 3 1 6 3 4 0 9 5 2 12 7 13 14 1 3 14 2 10 17 7 8 1 15 11 19 29 26 20 7 18 10 24 19 2 19 29 29 9 21 42 0 19 24 44 26
テスト出力3
50 14 13 18 7 7 8 7 2 6 3 2 6 2 5 2 1 2 2 8 2 2 1 1 3 1 3 1 1 4 1 1 1 1 1 1 1 1 1 1 1 1 3 1 2 1 1 1 1 1
解答例
必ず自分で問題に挑戦してみてから見てください。
クリックで解答例を見る
#include <bits/stdc++.h>
using namespace std;
// x番の組織が親組織に提出する枚数を返す
// childrenは組織の関係を表す2次元配列(参照渡し)
int count_report_num(vector<vector<int>> &children, int x) {
// ベースケース
if (children.at(x).size() == 0) {
// 子組織から受け取ることは無いので1枚であることが確定している
return 1;
}
// 再帰ステップ
int sum = 0;
for (int c : children.at(x)) {
sum += count_report_num(children, c);
}
sum += 1; // x番の組織の報告書の枚数(1枚)を足す
return sum;
}
// これ以降の行は変更しなくてよい
int main() {
int N;
cin >> N;
vector<int> p(N); // 各組織の親組織を示す配列
p.at(0) = -1; // 0番組織の親組織は存在しないので-1を入れておく
for (int i = 1; i < N; i++) {
cin >> p.at(i);
}
// 組織の関係から2次元配列を作る
vector<vector<int>> children(N); // ある組織の子組織の番号一覧
for (int i = 1; i < N; i++) {
int parent = p.at(i); // i番の親組織の番号
children.at(parent).push_back(i); // parentの子組織一覧にi番を追加
}
// 各組織について、答えを出力
for (int i = 0; i < N; i++) {
cout << count_report_num(children, i) << endl;
}
}