すべてのリンゴを箱に入れるとき

最初に、すべてのリンゴを箱に入れるために、どのくらい移動距離がかかるのかを考えてみましょう。

まずは移動距離の下界について考えます。座標 \(x\) の点（\(x\) は \(0\) 以上「一番右のリンゴ・箱の座標」以下）を通る回数は以下のようになります。

• 座標 \(x\) より左にあるリンゴの個数を \(c_a\)、箱の個数を \(c_b\) とする
  • \(c_a - c_b \geq 2\) のとき、リンゴを \(c_a - c_b\) 回以上右に送る必要があるため、\(2(c_a - c_b)\) 回以上通る
  • \(c_b - c_a \geq 2\) のとき、リンゴを \(c_a - c_b\) 回以上左に送る必要があるため、\(2(c_b - c_a)\) 回以上通る
  • それ以外のときでも、\(2\) 回以上通る

例えば下図のケースでは、区間 \([0, 2]\)（座標が \(0\) 以上 \(2\) 以下の区間）は \(2\) 回、区間 \([2, 3]\) は \(4\) 回、区間 \([3, 8]\) は \(2\) 回通る必要があるので、移動距離の下界が \(18\) と求まります。

一方、これで得られる下界と同じ移動距離を実際に達成する方法があります（以下の図の方法に対応しています）。

• 左から \(1, \dots, N\) 番目のリンゴを、それぞれ左から \(1, \dots, N\) 番目の箱に入れる
• 右方向に移動するリンゴについては、左側にあるものから順に箱に入れる
• 左方向に移動するリンゴについては、右側にあるものから順に箱に入れる

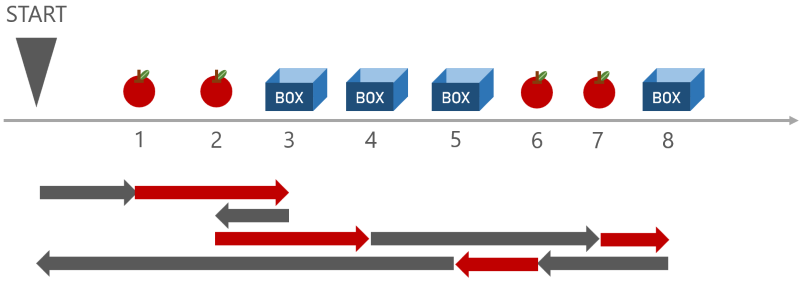
このように、リンゴと箱の個数の差を考えることで、最適な移動距離を求めることができます。

さて、元の問題に戻ってみましょう。上の考察を使うと、計算量 \(O(N^3)\) の以下のような DP を導出できます。

• \(dp[x][y][z]\): 座標 \(0\) から \(x\) まで見た時点で \(y\) 個のリンゴと \(z\) 個の箱を「使う」と決めたときの、現時点での移動距離（各点を通る必要回数を合わせることで計算される）の最小値

\(x\) として \(0, A_1, \dots, A_N, B_1, \dots, B_N\) しか考える必要がないので、DP の状態数は \(O(N^3)\) となります。しかし、これでは \(N \leq 4500\) の制約では TLE となってしまいます。

---

最適解の構造を考える

競技プログラミングでは、最適解が持つ構造を利用することで、問題が簡単になったり、高速化のアイデアが得られる場合があります。

ここでは、\(N\) 個中 \(K\) 個のリンゴを箱に入れるときに、移動距離いくつ必要か、という問題を考えます。

下図の例を考えます。これでは、途中の座標 \(4\) にあるリンゴを取らないせいで、座標 \(3\) から \(5\) までを \(6\) 回通る必要が出てしまっているので、直感的には最適ではないように見えます。

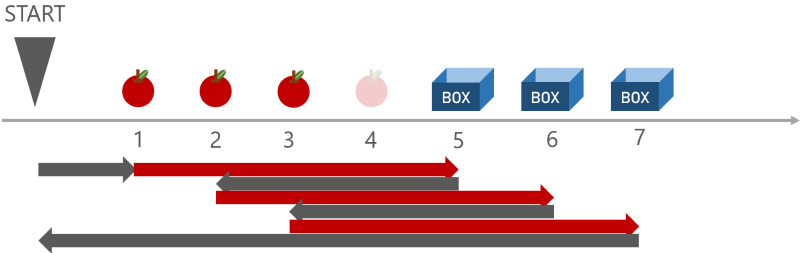
実際にこれは正しく、一般的に以下の性質が成り立ちます。

性質　「使わないリンゴまたは箱」であって、それより左にある「使うリンゴ」と「使う箱」の個数が異なるものが存在する場合、移動方法は最適ではない。

証明

移動距離が最小になる操作方法の中で、移動する各リンゴに対する「リンゴとそれを入れる箱の距離」の合計が最小になるものを「真の最適解」と定義します。

仮に、使わないリンゴであって、それより左にある「使うリンゴ」の個数が「使う箱の個数」より多い（★）とします（上図のケース ／ それ以外のケースも同様に証明できる）。使わないリンゴの座標を $x$ とします。

このとき、（★）の仮定より、座標 $x$ より左のリンゴを、座標 $x$ より右の箱に移動させる、というものが存在します。操作方法を「そのリンゴを取る代わりに座標 $x$ のリンゴを取る」と修正して、距離が短くなることはありません。さらに「リンゴとそれを入れる箱の距離」が真に短くなります。よって、元々の解は真の最適解ではありません。

よって、最適解で使うリンゴと箱の集合は、下図のように「リンゴと箱の数が同じである区間」をいくつか選んだもの、として表すことができます。

---

計算量 \(O(N^2)\) の DP

上の考察で、リンゴと箱の個数が同じである区間を前から順に選んでいく、というようにできるので、以下のような DP を導出できます。

• \(dp[x][y]\): 座標 \(x\) まで見た時点で \(y\) 個のリンゴと \(y\) 個の箱を使ったときの、現時点での移動距離（各点を通る必要回数を合わせることで計算される）の最小値

ここで、\(dp[x'][y']\) から \(dp[x][y]\) の遷移で、座標 \(x'\) から \(x\) までのリンゴと箱をすべて取る（ただしこの間にリンゴと箱がそれぞれ \(y-y'\) 個ずつあるとする）場合をカバーします。

しかし、リンゴと箱の個数が同じであるような区間は \(O(N^2)\) 通りあるので、この DP の最悪計算量は \(O(N^3)\) になってしまいます。

ここで、最悪ケースは、リンゴを A、箱を B として ABABABAB...AB と並んでいる場合です。このケースでは、例えば ABABAB の部分を一気に選ぶ、ということは、AB, AB, AB、と分けて選ぶのと同じになります。したがって「これ以上分解できない区間」のみを対象とすることで、このケースでは考えるべき区間が AB と BA の部分のみ（\(2N-1\) 通り）に減らせます。

実は、一般のケースでも「これ以上分解できない区間」は高々 \(2N\) 通りになります。理由は、各文字に対して、これから始まる「これ以上分解できない区間」の終点は一意に決まるからです（スタックの操作を考えれば分かりやすいです）。この工夫によって、DP の計算量を \(O(N^2)\) に減らせました。

---

実装例

• https://atcoder.jp/contests/ajo2024-final/submissions/60706910 (C++)