E - Five Shuffles Editorial by E869120
ステップ 1
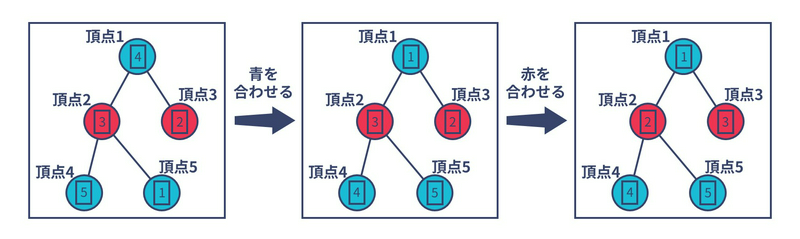
木を下図のように、隣接する頂点が同じ色にならないように青と赤の \(2\) 色で塗ることを考えます。また、頂点 \(x\) の色が青のとき整数 \(x\) を青の整数、頂点 \(x\) の色が赤のとき整数 \(x\) を赤の整数と呼ぶことにします。たとえば下図の場合、\(1\) は青の整数であり、\(2\) は赤の整数です。

すると、もしすべての青の頂点に青の整数が、すべての赤の頂点に赤の整数が書かれているような状態になっている場合、下図のように \(2\) 回の操作で「頂点 \(i\) に \(i\) が書かれている状態」にすることができます。
同様に、もし少なくとも \(N-2\) 個の頂点について「頂点の色と整数の色が一致している状態」にすることができれば、\(2\) 回の追加の操作で本問題の目的を達成できます。ここで、本問題では \(N\) 個全部一致している必要はなく、\(N-2\) 個で十分であることに注意してください。
問題は、いかにして「頂点の色と整数の色が \(N-2\) 頂点以上一致している状態」を作るかです。果たしてどうするのでしょうか。
ステップ 2
解法のカギは、木の重心に着目することです。
まず、頂点の色と整数の色が一致しているような頂点の重みを \(0\)、そうでない頂点の重みを \(1\) としたときの木の重心を核心と呼ぶことにします。たとえば下図上の場合、核心は頂点 \(3\) です。また下図下の場合、核心は頂点 \(2, 3, 4\) のいずれかです。
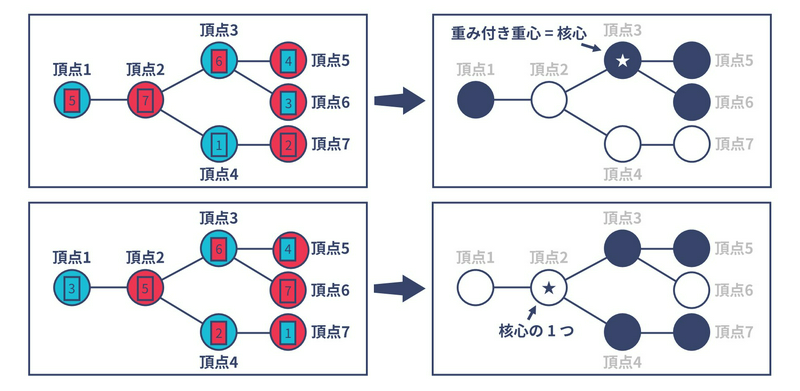
ここで核心の色については、以下の \(2\) パターンに場合分けされます。
- 核心について、頂点の色と整数の色が一致している。
- 核心について、頂点の色と整数の色が一致していない。
そこで、前者のケースで完全解 (\(N\) 頂点すべてについて頂点 \(i\) に書かれた整数が \(i\)) を達成することができれば、後者のケースも簡単に \(N-2\) 頂点一致を達成することができるので、以降は前者で完全解を目指す場合のみを考えます。すなわち、前者のケースについて、残る \(3\) 回の操作で「すべての頂点について、頂点の色と整数の色が一致する状態」を作り上げることを考えます。
パターン 1: 核心の次数が 2
まずは最も簡単なケースから考えます。核心の次数が \(2\) の場合、次のような操作をすれば良いです。ただし、核心を根とする根付き木を考えたときに、核心に接続する \(2\) つの部分木をそれぞれ「部分木 1」「部分木 2」と呼ぶことにします。
- 部分木 1 内で、赤の頂点に青の整数が書かれている頂点集合を \(S_1\)、青の頂点に赤の整数が書かれている頂点集合を \(T_1\) とする
- 部分木 2 内で、赤の頂点に青の整数が書かれている頂点集合を \(S_2\)、青の頂点に赤の整数が書かれている頂点集合を \(T_2\) とする
- このとき \(|S_1| = |T_2|\) および \(|S_2| = |T_1|\) が成り立つ
- そこで以下の \(2\) 回の操作を行うと良い
- \(S_1 \cup T_2\) に対してシャッフルを施し、\(S_1\) と \(T_2\) について色が一致するようにする
- \(S_2 \cup T_1\) に対してシャッフルを施し、\(S_2\) と \(T_1\) について色が一致するようにする
パターン 2: 核心の次数が 3
少し難しくなります。核心の次数が \(3\) の場合、以下のような操作をすれば良いです。ただし、核心を根とする根付き木を考えたときに、核心に接続する \(3\) つの部分木をそれぞれ「部分木 1」「部分木 2」「部分木 3」と呼ぶことにします。
- 部分木 1 内で、赤の頂点に青の整数が書かれている頂点集合を \(S_1\)、青の頂点に赤の整数が書かれている頂点集合を \(T_1\) とする
- 部分木 2 内で、赤の頂点に青の整数が書かれている頂点集合を \(S_2\)、青の頂点に赤の整数が書かれている頂点集合を \(T_2\) とする
- 部分木 3 内で、赤の頂点に青の整数が書かれている頂点集合を \(S_3\)、青の頂点に赤の整数が書かれている頂点集合を \(T_3\) とする
- このとき、以下の \(3\) 回の操作を行えば良い
- シャッフルを施し、\(S_1\) のうち \(a+b\) 個、\(T_2\) のうち \(a\) 個、\(T_3\) のうち \(b\) 個について色が一致するようにする
- シャッフルを施し、\(S_2\) のうち \(c+d\) 個、\(T_3\) のうち \(c\) 個、\(T_1\) のうち \(d\) 個について色が一致するようにする
- シャッフルを施し、\(S_3\) のうち \(e+f\) 個、\(T_1\) のうち \(e\) 個、\(T_2\) のうち \(f\) 個について色が一致するようにする
- ここで非負整数の組 \((a, b, c, d, e, f)\) は以下の制約を満たす必要があるが、\(|S_1| + |S_2| + |S_3| = |T_1| + |T_2| + |T_3|\) が満たされかつどの \(|S_i| + |T_i|\) も全体の半分を超えないため、このような組は存在する
- \(a+b=|S_1|\)
- \(c+d=|S_2|\)
- \(e+f=|S_3|\)
- \(d+e=|T_1|\)
- \(a+f=|T_2|\)
- \(b+c=|T_3|\)
たとえば \(|S_1| = 10, |S_2| = 7, |S_3| = 9, |T_1| = 5, |T_2| = 7, |T_3| = 14\) の場合、\((a, b, c, d, e, f) = (1, 9, 5, 2, 3, 6)\) とすれば良いです。なお、適切な \((a, b, c, d, e, f)\) の組は貪欲法を使って求めることができます。
パターン 3: 核心の次数が 4 以上の場合
最後は次数が \(4\) 以上の場合ですが、「頂点の色と整数の色が一致しない頂点の個数」が少ない \(2\) つの部分木をマージする、という操作を繰り返すと、どの部分木も全体の半分を超えないように次数 \(3\) の場合に帰着することができます。
例として、次数が \(7\) であり、各部分木における「頂点の色と整数の色が一致しない頂点の個数」が \(3, 4, 7, 9, 10, 13, 20\) であるとき、マージ過程は以下のようになります。
- \((3, 4, 7, 9, 10, 13, 20)\)
- \(\rightarrow (3+4, 7, 9, 10, 13, 20)\)
- \(\rightarrow (9, 10, 13, 3+4+7, 20)\)
- \(\rightarrow (13, 3+4+7, 9+10, 20)\)
- \(\rightarrow (9+10, 20, 3+4+7+13)\)
以上の場合分けをすると、ついに最大 \(5\) 回の独立集合シャッフルで本問題を解くことができます。解かれた方はおめでとうございます。
実装例 (C++)
posted:
last update: