C - Human Exercise Editorial by evima
Step 1: Focus on Symmetry
First, in this problem the path taken during each exercise is always symmetric with respect to the line passing through cells \((1, N), \dots, (N, 1)\). This can be observed from the diagram in the sample input, for example.
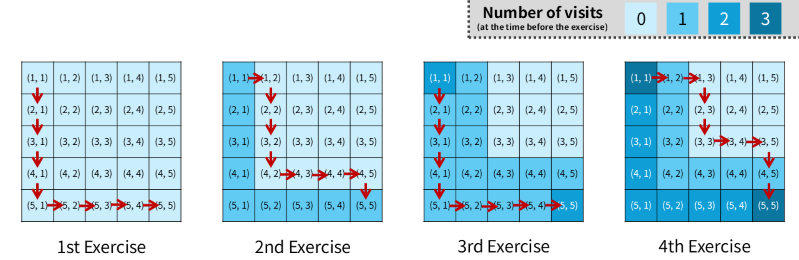
Therefore, if we know the first \(N-1\) moves (that is, the path until reaching one of \((1, N), \dots, (N, 1)\)), we can determine the remaining \(N-1\) moves as well. In other words, we only need to solve the “triangle version” of the problem that considers only those cells \((i, j)\) satisfying \(i + j \leq N+1\).
Step 2: The movement direction from each cell is actually periodic
From here on, we consider the triangle version of the problem.
Next, we explain the essence of this problem. In fact, for each cell \((i, j)\), the direction moved immediately after the \(1^{\text{st}}, 2^{\text{nd}}, 3^{\text{rd}}, \dots\) visits repeats the pattern
DDD...DDRRR...RR
(i.e.\ \(i\) times D followed by \(j\) times R), and then repeats.
Illustration of this property
It may be easiest to grasp by considering the case $(i, j) = (1, 1)$. The sequence of moves from this cell is ``` DRDRDRDR... ``` The reason is that starting from the state where cells $(1, 2)$ and $(2, 1)$ have been visited the same number of times, moving `D` makes the count for $(1, 2)$ one greater, then moving `R` returns to the state where the visit counts are equal, and this repeats.This property holds for all cells, not just $(1, 1)$.
Step 3: Use dynamic programming (DP) to compute the answer
Using the insight from Step 2, we can use DP to calculate the number of times each cell is visited in \(t\) exercises. Consider the following DP:
- \(\mathrm{dp}[i][j]\): the number of times cell \((i, j)\) is visited in \(t\) exercises
The base case is \(\mathrm{dp}[1][1] = t\). Other values are computed as shown in the diagram below by considering how many times “flow” moves from cell \((i, j)\) to the next cells (the example in the diagram is for \(N = 5, t = 100\)).
For example, if cell \((1, 3)\) is visited 33 times, then in the first 33 moves of the pattern DRRRDRRRDRRR..., D appears 9 times and R appears 24 times, so from here it moves to cells \((2, 3)\) and \((1, 4)\) 9 and 24 times, respectively.
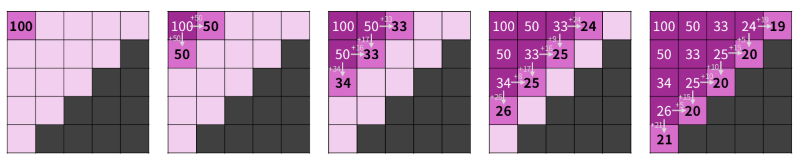
In this problem, we set \(t = K - 1\) when computing the DP values. Then we can simulate the moves on the \(K\)-th exercise to determine the answer. Hence, this problem can be solved in \(O(N^2)\) time complexity.
Proof of the solution
First, consider the triangle version of the problem. In this problem, there is the property that the movement directions at each cell are periodic, and we used this to solve the problem. Below, we prove this property.
The key idea in the proof is that the difference \(\mathrm{dp}[i+1][j] - \mathrm{dp}[i][j+1]\) is always either \(0\) or \(1\) (which can be seen by observing the diagram above). If we accept this fact, we can prove as follows that the DP values indeed match the actual visit counts for each cell.
Proof
First, define:
- \(a^{(t)}_{i, j}\): the number of times cell \((i, j)\) is visited in \(t\) exercises under the actual rules
- \(b^{(t)}_{i, j}\): the number of times cell \((i, j)\) is visited in \(t\) exercises when moving according to the rule (★) that the directions at each cell repeat
RR...RDD...D
- that is, the visit counts obtained by the DP in Step 3
- Here, assume that for any \(t, i, j\), we have \(0 \leq b^{(t)}_{i+1, j} - b^{(t)}_{i, j+1} \leq 1\).
We need to show that \(a^{(t)} = b^{(t)}\) for any \(t\). We prove this by induction on \(t\).
For \(t = 0\), we have \(a^{(t)}_{i, j} = b^{(t)}_{i, j} = 0\), so the statement holds trivially.
Assume \(a^{(t)} = b^{(t)}\). We show \(a^{(t+1)} = b^{(t+1)}\) as follows.The following properties hold for \(b^{(t+1)}_{i, j}\):
- The set of cells \((i, j)\) for which \(b^{(t+1)}_{i, j} - b^{(t)}_{i, j} = 1\) forms the path taken on the \((t+1)\)-th move under the rule ★ (for all other cells, \(b^{(t+1)}_{i, j} - b^{(t)}_{i, j} = 0\)).
- \(0 \leq b^{(t+1)}_{i+1, j} - b^{(t+1)}_{i, j+1} \leq 1\) holds.
Now, among the \(2^{N-1}\) ways to increase the value of \(b^{(t)}_{i, j}\) by \(1\) at a time along a path, which one satisfies condition 2? It turns out that the only possibility is to follow the exercise rule. This is because if, at cell \((i, j)\), we had \(b^{(t)}_{i+1, j} - b^{(t)}_{i, j+1} = 0\) and we moved right, the difference would become \(-1\), and if we had \(b^{(t)}_{i+1, j} - b^{(t)}_{i, j+1} = 1\) and we moved down, the difference would become \(2\), in either case violating condition 2.
Therefore, the set of cells in 1. is precisely the path taken under the exercise rule. Hence, \(a^{(t+1)} = b^{(t+1)}\) holds.
Next, we prove that each difference is indeed either \(0\) or \(1\). Here, we consider the case \(i, j \geq 1\) and assume that the differences \(b^{(t)}_{i+1,\,j-1} - b^{(t)}_{i,j},\quad b^{(t)}_{i,j} - b^{(t)}_{i-1,\,j+1}\) are each \(0\) or \(1\), and we prove that
\(b^{(t)}_{i+1,\,j} - b^{(t)}_{i,\,j+1}\) is also \(0\) or \(1\). This can be proved relatively straightforwardly by case analysis. Then, by induction on \(i+j\), one shows that all differences are either \(0\) or \(1\).
Handling the cases \(i = 0\) or \(j = 0\)
By defining \(b_{-1,k+1} = b_{0,k}\) and \(b_{k+1,\,-1} = b_{k,0}\), the proof proceeds similarly to the case \(i, j \geq 1\).
Proof that the difference is at least \(0\)
The case that minimizes \(b^{(t)}_{i+1, j} - b^{(t)}_{i, j+1}\) is when \(b^{(t)}_{i+1, j-1}, b^{(t)}_{i, j}, b^{(t)}_{i-1, j+1} = (x, x, x)\) (that is, the differences are \(0, 0\)).
Now, consider repeating the operation of moving simultaneously from \((i+1, j-1)\), \((i, j)\), \((i-1, j+1)\) to the next cells (under rule ★) \(x\) times. This becomes periodic with period length \(i+j+2\), and the directions of the moves in each cycle are:
Thus, in each cycle, both cells \((i+1,j)\) and \((i,j+1)\) are basically visited once, but exceptionally, only \((i+1,j)\) is visited once in the \((i+1)\)-th move, and only \((i,j+1)\) is visited on the \((i+2)\)-th move. Hence, the difference is \(1\) only when the remainder of \(x\) divided by \(i+j+2\) is \(i+1\), and \(0\) otherwise. It never becomes negative.
Proof that the difference is at most \(1\)
This can be proved in almost the same way as the proof that the difference is at least \(0\).
The case that maximizes \(b^{(t)}_{i+1, j} - b^{(t)}_{i, j+1}\) is when \(b^{(t)}_{i+1, j-1}, b^{(t)}_{i, j}, b^{(t)}_{i-1, j+1} = (x+2, x+1, x)\) (that is, the differences are \(1, 1\)). Here, first perform \(2\) and \(1\) moves respectively from \((i+1, j-1)\) and \((i, j)\) (under rule ★), and then consider repeating the operation of moving simultaneously from \((i+1, j-1)\), \((i, j)\), and \((i-1, j+1)\) to the next cells \(x\) times. This repeating operation has period length \(i+j+2\), and the directions of the moves in each cycle are:
Thus, in each cycle, both cells \((i+1,j)\) and \((i,j+1)\) are visited once, but exceptionally, only \((i,j+1)\) is visited once in the \((i+j+1)\)-th move, and only \((i+1,j)\) is visited once in the \((i+j+2)\)-th move. Taking into account that in the initial operations \((i+1,j)\) and \((i,j+1)\) are visited \(1\) and \(0\) times respectively, the difference becomes \(0\) only when the remainder of \(x\) divided by \(i+j+2\) is \(i+j+1\), and \(1\) otherwise. It never becomes \(2\) or greater.
This completes the proof of correctness for the triangle version of the problem. Finally, we prove the symmetry property for the original (square) version of the problem and conclude this section.
Proof of symmetry
Define \(a^{(t)}_{i, j}\) as the number of times cell \((i, j)\) is visited in \(t\) exercises. We prove symmetry by induction on \(t\). The case \(t = 0\) is trivial. Suppose for \(t \geq 0\) the symmetry \(a^{(t)}_{i, j} = a^{(t)}_{N-j-1, N-i-1}\) holds. We show that symmetry holds for \(t+1\) as well.
First, denote the path of the \((t+1)\)-th walk as \((1, 1) \to (r_1, c_1) \to \dots \to (r_{2N-1}, c_{2N-1})\) and prove that this path is symmetric. Here, we show that the direction of \((r_{N-1},c_{N-1}) \to (r_N,c_N)\) is different from that of \((r_N,c_N)\to(r_{N+1},c_{N+1})\). Define \((X, Y, Z) = (a^{(t)}_{r_{N-1}+1, c_{N-1}-1}, a^{(t)}_{r_{N-1}, c_{N-1}}, a^{(t)}_{r_{N-1}-1, c_{N-1}+1})\) (see the figure below). From the result already shown for the triangle version, the differences \(X - Y\) and \(Y - Z\) are each either \(0\) or \(1\). After the \((t+1)\)-th walk, only \(Y\) increases by 1, and the differences must still be either \(0\) or \(1\), implying \(X - Y = 1\) and \(Y - Z = 0\).

By the induction assumption on symmetry, there are three cells \((i, j)\) with \(i+j = N+2\) that correspond to \(X, Y, Z\) (see the figure above). Then:
- If \((r_{N-1},c_{N-1}) \to (r_N,c_N)\) is downward, moving down from \((r_N,c_N)\) leads to \(X\) and moving right leads to \(Y\). Since \(X - Y = 1\), the move from \((r_N,c_N)\) must be right.
- If \((r_{N-1},c_{N-1}) \to (r_N,c_N)\) is to the right, moving down from \((r_N,c_N)\) leads to \(Y\) and moving right leads to \(Z\). Since \(Y - Z = 0\), the move from \((r_N,c_N)\) must be down.
Since the only cells where \(a^{(t+1)}_{i, j}\) differs from \(a^{(t)}_{i, j}\) are those visited during the \((t+1)\)-th walk, which is symmetric, so symmetry holds for \(a^{(t+1)}\) as well.
Therefore, all walking paths are symmetric, and symmetry holds for \(a^{(t)}\) for all \(t\).
Sample implementation (C++)
#include <string>
#include <vector>
#include <iostream>
using namespace std;
// Function to compute the answer
string solve(int N, long long K) {
// step #1. Dynamic programming
vector<vector<long long>> dp(N);
for (int i = 0; i < N; i++) {
dp[i].resize(N - i);
}
dp[0][0] = K - 1;
for (int d = 0; d < N - 1; d++) {
for (int i = 0; i <= d; i++) {
int j = d - i; // Consider the flow from cell (i, j)
long long p = dp[i][j] / (d + 2);
int q = dp[i][j] % (d + 2);
dp[i + 1][j] += (i + 1) * p + min(q, i + 1);
dp[i][j + 1] += (j + 1) * p + max(q - (i + 1), 0);
}
}
// step #2. Simulate the K-th walk
string ans;
int r = 0, c = 0;
for (int i = 0; i < N - 1; i++) {
if (dp[r + 1][c] <= dp[r][c + 1]) {
ans += 'D';
r += 1;
} else {
ans += 'R';
c += 1;
}
}
// step #3. Use symmetry to determine the second half of the path
for (int i = N - 2; i >= 0; i--) {
if (ans[i] == 'D') {
ans += 'R';
} else {
ans += 'D';
}
}
return ans;
}
int main() {
int N; long long K;
cin >> N >> K;
string ans = solve(N, K);
cout << ans << endl;
return 0;
}
posted:
last update: