How did you enjoy this contest? It may be arguably the hardest AGC ever. Let us dive into the editorial.

---

Step 1: Rephrasing as a scheduling problem

In competitive programming, you can sometimes make a problem easier by looking at it from a different angle. This problem can be rephrased as the following scheduling problem:

Problem: There are \(N\) tasks. Task \(i\ (1 \leq i \leq N)\) is released at time \(T_i - X_i\) and must be worked on for consecutive \(2X_i\) seconds, finishing no later than time \(T_i + D + X_i\). Determine whether all tasks can be completed.

Here, a single “go from coordinate 0, press the button, and return to 0” trip is regarded as “working on one task.” Thinking in terms of everyday homework or work tasks is often more intuitive than thinking in terms of coordinates.

---

Step 2: Ignore release times first

Jumping straight to a full solution is hard, so first ignore the release‑time constraints (imagine every task is released at time 0).

In that situation, processing the tasks in non‑decreasing order of deadlines is optimal. If that schedule fits within every deadline, the answer is Yes; otherwise, it is No. The optimality is proven with the classic swap argument: if any two consecutive tasks are out of deadline order yet the schedule still fits, swapping them keeps every deadline satisfied, so we can keep swapping until the list is fully sorted by deadline.

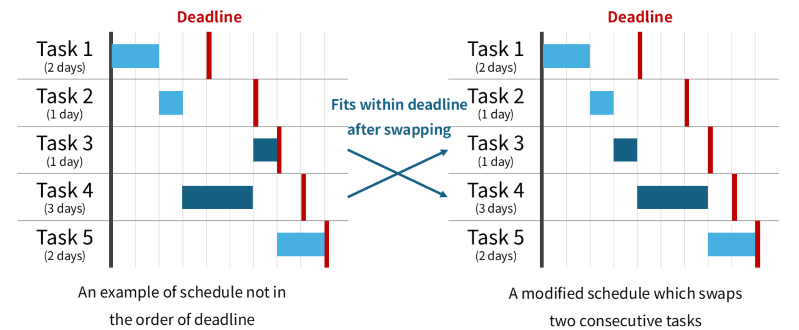
Formal proof

Let task $i$ take $c_i$ seconds and have deadline $d_i$, and assume they are sorted so that $d_1 \le \dots \le d_N$.

Suppose the order $p_1,\dots,p_N$ works. If this order is not $(1,2,\dots,N)$ there exists an index $i$ with $p_i > p_{i+1}$. Swapping these two still satisfies all deadlines because:

• Every other task’s start/finish times stay unchanged.
• Task $p_{i+1}$ finishes no later than its deadline in the original schedule; that remains true after the swap.
• Since $p_i > p_{i+1}$, we have $d_{p_i} \ge d_{p_{i+1}}$, so $p_i$’s deadline is even later.

Repeating swaps until the sequence is $(1,2,\dots,N)$ shows that if the deadlines are met using $p \neq (1, 2, \dots, N)$, they would also be met using $p = (1, 2, \dots, N)$. Hence, sorting by deadline order is optimal.

---

Step 3: What changes when release times matter?

Now assume the tasks are already sorted by deadline, i.e. \(T_1 + X_1 \le \dots \le T_N + X_N\).

Unfortunately, the previous swap argument can break down: swapping can violate release times, and in fact the deadline order is sometimes not optimal.

Counter‑example

Let $N=2$. Task $1$ is available from time $3$ to $9$ and takes $2$ seconds; task $2$ is available from time $0$ to $10$ and takes $6$ seconds. Doing task $1$ first fails, but doing $2$ then $1$ succeeds.
This corresponds to $N=2,\ D=4,\ (T_1,X_1)=(4,1),\ (T_2,X_2)=(3,3)$.

Do we have to abandon swapping altogether? Not quite. We can still swap when the release constraint remains satisfied. The key is the following property, which fortunately does hold for this specific problem:

Property: For two tasks \(i_1 < i_2\), if we choose to do the later‑deadline task \(i_2\) before the earlier‑deadline task \(i_1\), then by the time \(i_2\) finishes, \(i_1\) is already released.

Proof: Task \(i_2\) starts no earlier than time \(T_{i_2}-X_{i_2}\) and lasts \(2X_{i_2}\) seconds, so it finishes no earlier than time \(T_{i_2}+X_{i_2}\).
Task \(i_1\) is released at time \(T_{i_1}+X_{i_1}\), and we have \(T_{i_1}+X_{i_1}\le T_{i_2}+X_{i_2}\), so it is indeed available.

Because of this property, we can perform swapping to hasten task \(i_1\), because as long as task \(i_1\) is done later than task \(i_2\), task \(i_1\) is already released when we start doing it, no matter what order we use. Therefore, whenever some remaining task has an earlier deadline than the one just completed, we should immediately process those earlier‑deadline tasks next, in order of deadline.

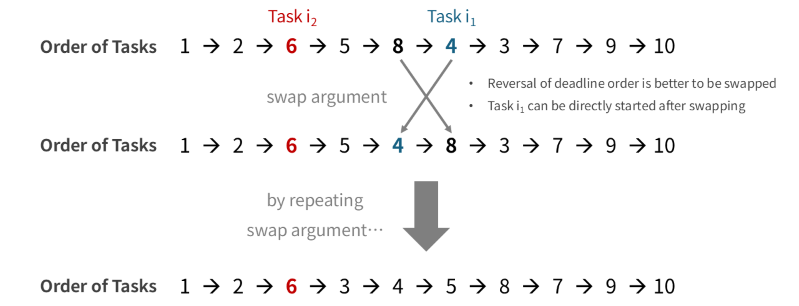
Optimal schedules thus have the following structure: pick any one task, and then finish all tasks with earlier deadlines in order, like \((1)\), \((2)\), \((6,3,4,5)\), \((8,7)\), \((9)\), \((10)\) in the diagram.

---

Step 4: Dynamic programming

This structure suggests a DP.

Let \(\mathrm{dp}[i] =\) the earliest possible finishing time after completing tasks \(1,2,\dots,i\) (or \(+\infty\) if impossible). The transition from \(\mathrm{dp}[j]\) to \(\mathrm{dp}[i]\) requires doing tasks \(i, j+1, j+2, \dots, i-1\) in that order. Simulating this naively costs \(O(N)\) time, for a total of \(O(N^3)\) to find all DP values. The answer is Yes if \(\mathrm{dp}[N] < \infty\).

Pseudo‑code:

// simulate doing tasks i, j+1, j+2, ..., i-1 in this order
function simulate(j, i):
	t := dp[j]
	t := max(t, T[i]-X[i]) // start task i
	t := t + 2*X[i] // do task i
	if t > T[i]+D+X[i]
		return INF
	for k = j+1, ..., i-1 do
		t := max(t, T[k]-X[k]) // start task k
		t := t + 2*X[k] // do task k
		if t > T[k]+D+X[k]
			return INF
	return t

// dynamic programming
dp = [0, INF, INF, ..., INF]
for j = 0, 1, ..., N-1 do
	for i = j+1, j+2, ..., N do
		res := simulate(j, i) // simulate transition
		dp[i] := min(dp[i], res)

// print the answer
print ("Yes" if dp[N] != INF, "No" otherwise)

---

Step 5: Speeding up the DP

With \(N \le 5\,000\), we need an \(O(N^2)\) solution.

Observe that when tasks \(i, j+1, \dots, i-1\) are done in this order, every intermediate task \(j+1,\dots,i-1\) can start immediately after the previous one finishes. Thus, in the psoudo-code above, line 9 t := max(t, T[k]-X[k]) is unnecessary. That is, if t has the value \(t_0\) at line 6, it will be \(t_0 + 2X_{j+1} + \dots + 2X_k\) at the end of a loop of \(k\). Hence:

1. The transition fails (the result is \(+\infty\)) if \(t_0 + 2X_{j+1} + \dots + 2X_k > T_k + D + X_k\) for some \(k = j+1, \dots, i-1\).
2. Otherwise, the last task finishes at time \(t_0 + 2X_{j+1} + \dots + 2X_{i-1}\).

Here, the condition for 1. can be rephrased as \(\max_{k = j+1, \dots, i-1} \{2X_{j+1} + \dots + 2X_k - (T_k + X_k)\} > D - t_0\). This cumulative max can be found in \(O(1)\) time for each \((j, i)\). The result of 2. can also be found in \(O(1)\) time using prefix sums. Thus, the simulation can be performed in \(O(1)\) time, for a total of \(O(N^2)\) to find all DP values.

---

Sample implementation (C++)

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

// Reorders array A according to perm
vector<long long> permute(int N, const vector<long long>& A, const vector<int>& perm) {
	vector<long long> res(N);
	for (int i = 0; i < N; i++) {
		res[i] = A[perm[i]];
	}
	return res;
}

// Returns true if the game is winnable
bool solve(int N, long long D, vector<long long> T, vector<long long> X) {
	// step #1. sort by T[i] + X[i]
	vector<int> ranking(N);
	for (int i = 0; i < N; i++) {
		ranking[i] = i;
	}
	sort(ranking.begin(), ranking.end(), [&](const int a, const int b) {
		return T[a] + X[a] < T[b] + X[b];
	});
	T = permute(N, T, ranking);
	X = permute(N, X, ranking);

	// step #2. dynamic programming
	const long long INF = 7LL << 58;
	vector<long long> dp(N + 1, INF);
	dp[0] = 0;
	for (int j = 0; j < N; j++) {
		long long sum = 0; // // maintain X[j] + ... + X[i-1]
		long long current_max = -INF; // maintain cum. max of 2X[j] + ... + 2X[k-1] - (T[k]+X[k])
		for (int i = j + 1; i <= N; i++) {
			long long t0 = max(dp[j], T[i - 1] - X[i - 1]) + 2 * X[i - 1];
			if (t0 <= T[i - 1] + D + X[i - 1]) {
				if (current_max <= D - t0) {
					long long finish = t0 + sum * 2;
					dp[i] = min(dp[i], finish);
				}
			}
			sum += X[i - 1];
			current_max = max(current_max, sum * 2 - (T[i - 1] + X[i - 1]));
		}
	}

	// the answer is Yes if dp[N] < INF
	return dp[N] < INF;
}

int main() {
	cin.tie(nullptr);
	ios::sync_with_stdio(false);
	int TESTCASES;
	cin >> TESTCASES;
	for (int id = 1; id <= TESTCASES; id++) {
		int N; long long D;
		cin >> N >> D;
		vector<long long> T(N), X(N);
		for (int i = 0; i < N; i++) {
			cin >> T[i] >> X[i];
		}
		bool ans = solve(N, D, T, X);
		cout << (ans ? "Yes" : "No") << '\n';
	}
	return 0;
}