E - Flights 2 解説 by square1001
ステップ 1A: 最初はパスグラフの場合を考えよう
競技プログラミングの問題を解くときに、解法が見えにくい場合は、単純なケースを考えるのが良い戦略です。解説のステップ 1A, 1B, 1C では、最も原始的なケースとしてパスグラフの場合(つまり、\(M = N - 1\) で、\(1 \to 2, 2 \to 3, \dots, (N-1) \to N\) の辺がある場合)を考えます。
これからいくつか具体的な例を考えてみましょう。
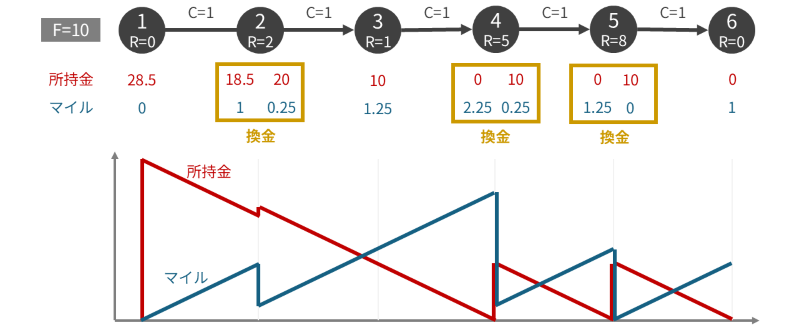
具体例 1 例えば、\(N = 6, F = 10, C_i = 1, R = (0, 2, 1, 5, 8, 0)\) のケースについて、最適解は以下の図のようになっています。
この結果を観察してみましょう。
- 空港 \(3\) では、換金を行わずに通過している
- 空港 \(5\) では、今あるマイルをすべて換金している
- 空港 \(2, 4\) では、次に換金する空港まで所持金がギリギリ持つように換金している
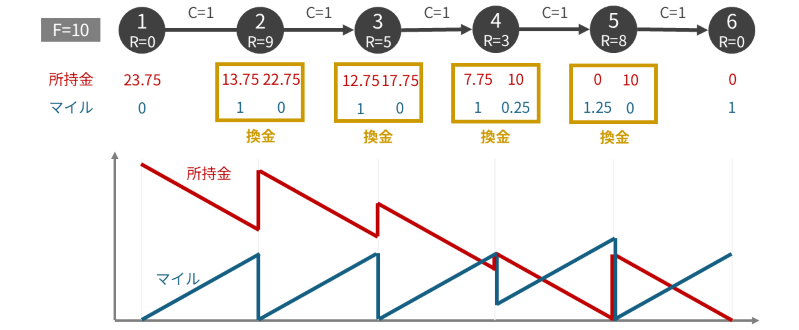
具体例 2 例えば、\(N = 6, F = 10, C_i = 1, R = (0, 9, 5, 3, 8, 0)\) のケースについて、最適解は以下の図のようになっています。
この結果を観察してみましょう。
- 空港 \(2, 3, 5\) では、今あるマイルをすべて換金している。
- 空港 \(4\) では、次に換金する空港まで所持金がギリギリ持つように換金している
ステップ 1B: 最適解の構造を探る
この 2 つの具体例の結果を見ると、最適解の以下の性質が見えてきます。これは、どんな場合でも成り立つのでしょうか?
性質 換金を行うときは、今あるマイルをすべて換金しているか (Type A)、次に換金する空港まで所持金がギリギリ持つように換金するか (Type B)、である。
実は、この性質は必ず成り立ちます。この直感的な理由は、Type A, B のどちらでもない換金を行う場合、換金するマイルをその空港と次の空港でどちらか一方向に一定量移し替えた方が所持金を増やせるからです。
厳密な証明
仮に、ある空港 \(x\) で Type A, B のどちらでもない換金をするとします。
このとき、以下のようにして解を改善できることが示されます。ここで、次の空港を \(y\) とし、\(\varepsilon > 0\) を十分小さい実数とします。
ここで、両方の “変化” が実現可能であることに注意しましょう。前者が実現可能なのは空港 \(x\) でマイルを全部換金するわけではないから、後者が実現可能なのは空港 \(x\) で次に換金する空港でも余裕があるように換金するからです。
問題は \(R_x = R_y\) の場合ですが、例えば「最初の所持金が同じでも換金を後回しにできる方が良い解である」というようにタイブレークをつけて最適性を定義すると、どちらか一方を行った方が解が改善できることになります。
以上より、最適解において 性質 が成り立ちます。
ここで、Type A はその空港を出発するときにマイルが 0 になること、Type B は次の空港に到着するときに所持金が 0 になることを意味します。これを図に表すと以下のようになります。
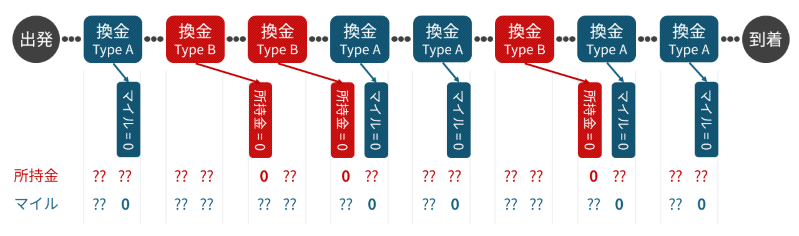
このように考えると、所持金が 0 でもマイルが 0 でもない換金が 2 連続で行われることがないことが分かります。より具体的には、以下のことが分かります。
- Type A → Type A のケース: マイルが 0 の状態からマイルが 0 の状態までは、途中の空港での換金が 0 回
- Type A → Type B のケース: マイルが 0 の状態から所持金が 0 の状態までは、途中の空港での換金が 1 回
- Type B → Type A のケース: 所持金が 0 の状態からマイルが 0 の状態までは、同じ空港で遷移する
- Type B → Type B のケース: 所持金が 0 の状態から所持金が 0 の状態までは、途中の空港での換金が 0 回
ステップ 1C: 動的計画法 (DP) でパスの場合を解く
ここでは、最初の所持金が \(x\) 円のときに空港 \(N\) に行くことは可能か判定する問題を考えます。元の問題の答えは \(x\) について二分探索することで求まります。
ステップ 1B の考察より、マイルが 0 の状態や所持金が 0 の状態を経由しながら換金を行っていくことになります。以下の値を計算する DP を考えます。
- \(\mathrm{dp}_1[i]\): 空港 \(i\) を出発する時点でマイルが \(0\) であるときの、その時点での所持金の最大値
- \(\mathrm{dp}_2[i]\): 空港 \(i\) に到着する時点で所持金が \(0\) であるときの、その時点でのマイルの最大値
\(\mathrm{dp}_1[j] \to \mathrm{dp}_1[i]\) の遷移、\(\mathrm{dp}_1[j] \to \mathrm{dp}_2[i]\) の遷移、\(\mathrm{dp}_2[j] \to \mathrm{dp}_1[i]\) の遷移、\(\mathrm{dp}_2[j] \to \mathrm{dp}_2[i]\) の遷移は、それぞれ Type A → Type A の遷移、Type A → Type B の遷移、Type B → Type A の遷移、Type B → Type B の遷移に対応しています。そのうち、\(\mathrm{dp}_1[j] \to \mathrm{dp}_2[i]\) の遷移のみ、途中の空港 \(k \ (j < k < i)\) で換金する必要があります。\(k\) を全探索する必要があるので、DP の値を全部計算するのに計算量 \(O(N^3)\) かかります。
以上より、パスグラフの場合の問題は計算量 \(O(N^3 \log \frac{1}{\varepsilon})\) で解けました(\(\varepsilon = 10^{-6}\) は許容誤差)。
ステップ 2A: 一般グラフへの拡張
一般グラフでも、換金についてパスグラフの場合と同様の性質(所持金が 0 でのマイルが 0 でもない換金が 2 連続で行われることがない、など)が成り立ちます。なので、ステップ 1C と同様に \(\mathrm{dp}_1[i]\) と \(\mathrm{dp}_2[i]\) を計算したいです。しかし、残念ながら、パスグラフの場合と違ってどの順番で \(\mathrm{dp}_1[i], \mathrm{dp}_2[i]\) を計算してよいかわからないという問題が生じます(実際には、グラフにサイクルが含まれる場合はあらかじめ決まった順番で計算することができません)。
ここで、最短経路問題のベルマン・フォード法で見るようなアイデアで DP の値を求めることを考えます。以下の値を計算する DP を考えます。
- \(\mathrm{dp}_1[t][i]\): 今まで行った換金の回数が \(t\) で、空港 \(i\) を出発する時点でマイルが \(0\) であるときの、その時点での所持金の最大値
- \(\mathrm{dp}_2[t][i]\): 今まで行った換金の回数が \(t\) で、空港 \(i\) に到着する時点で所持金が \(0\) であるときの、その時点でのマイルの最大値
このように換金回数 \(t\) を導入することで、\(t\) の小さい順に DP を計算すればよい、となりました。同じ空港で 2 回以上(別の空港に行った後にまた戻ってきて)換金するのは最適ではないので、\(t \leq N\) まで計算すればよいです。よって、計算量 \(O(N^4)\) で DP が求まります。これで、一般グラフの場合が計算量 \(O(N^4 \log \frac{1}{\varepsilon})\) で解けました。
ちなみに、DP の値を計算する際に「この空港からこの空港まで(換金せずに)行くのに何円必要か」を計算することになりますが、これはあらかじめ全点対間最短経路をワーシャル・フロイド法で計算量 \(O(N^3)\) で求めておくことで対処できます。
ステップ 2B: DP 高速化① - ベルマン・フォードからダイクストラへ
ステップ 2A では、ベルマン・フォード法の要領で \(\mathrm{dp}_1[i], \mathrm{dp}_2[i]\) の値を求めていましたが、この影響で計算量が遅くなってしまいました。自然な疑問として、ダイクストラ法の要領で求められないか、という問いが浮かび上がります。
ダイクストラ法の要領で DP の値を求めるためには、\(\mathrm{dp}_1[i], \mathrm{dp}_2[i]\) の値を適切な順番で “確定” させていき、そのたびに未確定の \(\mathrm{dp}_1[j], \mathrm{dp}_2[j]\) の値を(\(\mathrm{dp}_{?}[i] \to \mathrm{dp}_{?}[j]\) の遷移によって)”更新” していく、という流れで解くことになります。しかし、適切な順番とは何なのか、という問題が生じていました。
ここでちょうどよいところに、以下の性質があります。
性質 動作の過程において (所持金) + F × (マイル) は広義単調減少である。
性質の証明
2 つの動作それぞれについて証明します。
このため、(所持金) + F × (マイル) が大きい順に、つまり \(\mathrm{dp}_1[i]\) あるいは \(F \times \mathrm{dp}_2[i]\) の大きい順に DP の値を確定させていけばよいことになります。これで、DP の計算量が \(O(N^3)\) に改善しました。
これで、一般グラフの場合が計算量 \(O(N^3 \log \frac{1}{\varepsilon})\) で解けました。
ステップ 2C: DP 高速化② - 後ろから考える
いよいよ最後のステップです。ステップ 2B では、最初の所持金を二分探索していたために \(\log \frac{1}{\varepsilon}\) 倍の計算量がかかっていました。これを解消するために、空港 \(1\) からではなく空港 \(N\) から経路を逆順にたどるように DP を作ってみましょう。以下の値を計算する DP を考えます。
- \(\mathrm{dp}'_1[i]\): 空港 \(i\) を出発する時点でマイルが \(0\) であるときに、空港 \(N\) に行くのに必要なその時点での所持金の最小値
- \(\mathrm{dp}'_2[i]\): 空港 \(i\) に到着する時点で所持金が \(0\) であるときに、空港 \(N\) に行くのに必要なその時点でのマイルの最小値
DP は先ほどとは逆の順序で計算することになります。例えば、Type A → Type A の遷移では、「空港 \(i\) を出発する時点で所持金 \(\mathrm{dp}'_1[i]\) + マイル \(0\) にするために、空港 \(j\) を出発する時点で所持金いくつ(+ マイル \(0\))持っている必要があるか?」(この答えはグラフの \(j \to i\) の距離を \(d\) として \(\max(\mathrm{dp}'[i] - d \times R_i, 0) + F \times d\) となる)といった値を計算することになります。また、ダイクストラ法の要領で計算する際には、\(\mathrm{dp}'_1[i]\) または \(F \times \mathrm{dp}'_2[i]\) の小さい順に DP の値を確定させていくことになります。
本問題の答えは \(dp'_1[1]\) です。これで二分探索を解消でき、この問題を計算量 \(O(N^3)\) で解くことができました。
実装例 (C++)
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int INF = 1012345678;
// グラフの全点対間最短距離をワーシャル・フロイド法で求める関数
vector<vector<int> > warshall_floyd(int N, vector<vector<int> > C) {
for (int i = 0; i < N; i++) {
C[i][i] = 0;
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
C[j][k] = min(C[j][k], C[j][i] + C[i][k]);
}
}
}
return C;
}
// 問題を解く関数
double solve(int N, int F, const vector<vector<int> >& C, const vector<int>& R) {
// step #1. ダイクストラ法:準備
vector<vector<int> > d = warshall_floyd(N, C); // 全点対間最短距離
vector<double> dp1(N, 1.0e+99), dp2(N, 1.0e+99); // DP の値
vector<bool> used1(N, false), used2(N, false); // "確定" させたかのフラグ
dp1[N - 1] = 0.0;
// step #2. ダイクストラ法
while (true) {
// 確定させる頂点を選ぶ
double opt = 1.0e+99;
int tp = -1, u = -1;
for (int i = 0; i < N; i++) {
if (!used1[i] && opt > dp1[i]) {
opt = dp1[i];
tp = 1;
u = i;
}
if (!used2[i] && opt > dp2[i] * F) {
opt = dp2[i] * F;
tp = 2;
u = i;
}
}
// すべての頂点が確定していればダイクストラ法を終了
if (tp == -1) {
break;
}
// 頂点を確定させる
if (tp == 1) {
used1[u] = true;
} else {
used2[u] = true;
}
// dp2[?] <- dp1[u] の遷移
if (tp == 1) {
if (!used2[u] && R[u] != 0) {
dp2[u] = min(dp2[u], dp1[u] / R[u]);
}
}
// dp1[?] <- dp1[u] の遷移
if (tp == 1) {
for (int j = 0; j < N; j++) {
if (!used1[j] && d[j][u] != INF) {
double x = d[j][u] * F + max(dp1[u] - d[j][u] * R[u], 0.0);
dp1[j] = min(dp1[j], x);
}
}
}
// dp2[?] <- dp2[u] の遷移
if (tp == 2) {
for (int j = 0; j < N; j++) {
if (!used2[j] && d[j][u] != INF && R[j] != 0) {
double x = double(d[j][u] * F) / R[j] + max(dp2[u] - d[j][u], 0.0);
dp2[j] = min(dp2[j], x);
}
}
}
// dp1[?] <- dp2[u] の遷移
if (tp == 2) {
for (int j = 0; j < N; j++) {
if (d[j][u] != INF) {
if (dp2[u] <= d[j][u]) {
if (!used1[j]) {
double x = d[j][u] * F;
dp1[j] = min(dp1[j], x);
}
} else if (R[j] != 0) {
// 経由地があるパターン: k -> j -> u と行く(j が経由地)
for (int k = 0; k < N; k++) {
if (!used1[k] && dp2[u] <= d[j][u] + d[k][j]) {
double diff = (d[j][u] + d[k][j]) - dp2[u];
double money = d[j][u] * F - diff * R[j];
if (money > 0) {
money += d[k][j] * F;
dp1[k] = min(dp1[k], money);
}
}
}
}
}
}
}
}
// 答えは dp1[0]
return dp1[0];
}
int main() {
cin.tie(nullptr);
ios::sync_with_stdio(false);
int TESTCASES;
cin >> TESTCASES;
for (int id = 1; id <= TESTCASES; id++) {
int N, M, F;
cin >> N >> M >> F;
vector<vector<int> > C(N, vector<int>(N, INF));
for (int i = 0; i < M; i++) {
int a, b, c;
cin >> a >> b >> c;
a--; b--;
C[a][b] = min(C[a][b], c);
}
vector<int> R(N);
for (int i = 0; i < N; i++) {
cin >> R[i];
}
long double ans = solve(N, F, C, R);
cout.precision(16);
cout << fixed << ans << '\n';
}
return 0;
}
補足: 誤差の証明
この問題では浮動小数点数を使って答えの計算を行っていますが、前述の実装例では相対誤差が \(O(N \varepsilon)\) で抑えられることが証明できます。ここで、\(\varepsilon\) はマシンイプシロン(例えば double 型の場合は \(2^{-53}\))です。この事実は、4 パターンいずれの遷移の計算式も、実質的に \(\mathrm{dp}_?[?] \times (\text{正の定数}) + (\text{正の定数})\) と表せ(ここでの “定数” とは DP の値に依存しない数、という意味です)、この演算で増える相対誤差は \(O(\varepsilon)\) であるから、という議論で証明できます。
投稿日時:
最終更新: