Official

B - Insert 1, 2, 3, ... Editorial by maspy

ヒント → https://atcoder.jp/contests/agc063/editorial/6736

[1] 生成可能性の判定

列が生成可能であるというのは，操作を逆順に見れば，\(a\) から \((1,2,\ldots,k-1,k)\) の削除を繰り返して空列にできることと同値です．したがって，実際に \((1,2,\ldots,k-1,k)\) を可能な限り削除していって空列になるかどうかを調べるという判定方法が考えられます．

この際，どのような \((1,2,\ldots,k-1,k)\) を削除すべきかの選択肢が複数あるのが厄介ですが，この場所は次のように一意に定めることができます．

【命題】 \(a\) を空でない列とし，その中で最も右にある \(1\) に注目する．この \(1\) から始まる最大長の連番が \((1, 2, \ldots, k)\) であるとし，\(a'\) を \(a\) からこの連番を削除した列であるとする． このとき，\(a\) が生成可能であることと \(a'\) が生成可能であることは同値である．

\(a'\) が生成可能ならば \(a\) が生成可能であることは明らかです．

\(a\) が生成可能であるとし最も右にある \(1\) から始まる最大長の連番を \((1,2,\ldots,k)\) とします．この \(1\) が削除されるまではこの位置より右で削除操作は行われません（最も右にある \(1\) に注目しているので）．よってこの \(1\) と同時に削除される連番を \((1,2,\ldots,k')\) とすれば \(k'\leq k\) が成り立ちます．

\(k'<k\) が成り立つとすると， \((1,2\ldots,k')\) が削除された以降のある操作で \((k'+1,k'+2,\ldots)\) 部分のいくつかが同時に削除されることになります．この削除操作を \((1,2,\ldots,k')\) 部分と同時に削除するように変更すれば，最も右にある \(1\) と同時に削除する数の個数を増やすことができます．これを繰り返せば，最大長の連番 \((1,2,\ldots,k)\) を同時に削除するような手順が得られます．

次の図も参考にしてください．

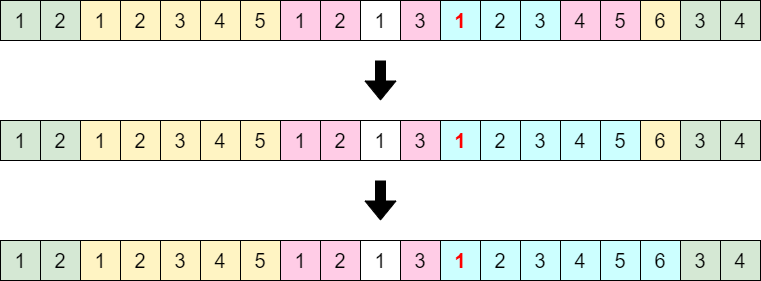
したがって列が生成可能であるかを判定するには，最も右にある \(1\) から始まる最大長の連番を削除することを繰りかえせばよいです．より具体的には，スタックを用いて次のようにすればよいです．

【判定アルゴリズム】

  • 列 \(a\) の右側の要素から順に，スタックに追加する．
  • \(1\) が追加されたとき，スタックの上から順に連番になっている部分の最大長を取り除く．
  • 列のすべての要素を処理し終えた時点でスタックが空であれば \(a\) は生成可能である．空でないならば \(a\) は生成可能ではない．

[2] 数え上げ

組 \((L,R)\) の個数を数える問題ですが，次の自然な 2 つの方法どちらでも解くことができます．計算量はいずれも \(O(N)\) 時間です．

[2-1] \(L\) を固定して数える

\(L\) を固定したときの条件を満たす \((L,R)\) の個数を求める問題を考えます．この際，次の単調性が役に立ちます．

  • \(L\leq R_1\leq R_2\) かつ \((L,R_2)\) が条件を満たすならば，\((L,R_1)\) も条件を満たす．

単調性より，各 \(L\) に対して条件を満たす最大の \(R\) が求められればよいです．この \(R\) は，[1] の【判定アルゴリズム】を \(A\) 全体に対して行ったときに，\(A_L\) を追加した直後のスタックの先頭を読むことで計算できます（スタックの先頭が，\(A_L\) までで削除できない最も左の要素になります）．

[2-2] \(R\) を固定して数える

\(R\) を固定したときの条件を満たす \((L,R)\) の個数を求める問題を考えます．これは，\((A_1, \ldots, A_R)\) 部分に [1] の【判定アルゴリズム】を \(A_R\) から行ったときに，スタックが空になることが何回あるかという問題です．

求める回数を \(\mathrm{dp}[R]\) とします．【判定アルゴリズム】を \((A_1, \ldots, A_R)\) 部分に行ったときに，\(A_L\) の挿入直後に初めてスタックが空になるとすると，\(\mathrm{dp}[R] = \mathrm{dp}[L-1] + 1\) の要領で計算できます．

したがって【判定アルゴリズム】を \((A_1, \ldots, A_R)\) 部分に行ったときにスタックが初めて空になるのはいつかが分かればよいです．これは【判定アルゴリズム】を \(A\) 全体に行ったときに初めて \(A_R\) が取り出されるタイミングそのものです．

posted:
last update: