We assume that you know Kirchhoff’s matrix tree theorem.

Let \(S\) be the number of vertices, and number them from \(1\) to \(S\) in some way.

Let \(A\) be an \(S\)-by-\(S\) matrix defined as follows.

• \(A\) is a diagonal matrix.
• \(A_{i,i}=\) (number of vertices connected to vertex \(i\) by an edge) \(+1\).

Also, let \(B\) be an \(S\)-by-\(S\) matrix defined as follows.

• \(B_{i,j}=\) \(1\) if the intervals written on vertices \(i\) and \(j\) intersect, and \(0\) otherwise. Note particularly that the diagonal consists of \(1\).

In the computation with the matrix tree theorem, we are interested in the matrix \((A-B)\) (with some rows and columns removed).

Let us make \(B\) seem easier to deal with by the following conversion. For each interval \([l,r]\) (\(1 \leq l \leq r \leq N\)), let column vectors \(F(l,r)\) and \(G(l,r)\) of length \(2N-1\) defined as follows.

• Let \(F(l,r)\) be the following vector \(v\).
  • \(v_{2i-1}=1\) (\(i \in [l,r]\))
  • \(v_{2i-1}=0\) (\(i \not \in [l,r]\))
  • \(v_{2i}=1\) (\([i,i+1] \subset [l,r]\))
  • \(v_{2i}=0\) (\([i,i+1] \not \subset [l,r]\))
• Let \(G(l,r)\) be the following vector \(v\).
  • \(v_{2i-1}=1\) (\(i \in [l,r]\))
  • \(v_{2i-1}=0\) (\(i \not \in [l,r]\))
  • \(v_{2i}=-1\) (\([i,i+1] \subset [l,r]\))
  • \(v_{2i}=0\) (\([i,i+1] \not \subset [l,r]\))

Let us simply denote by \(F(i)\) and \(G(i)\), respectively, the values of \(F\) and \(G\) corresponding to the interval written on vertex \(i\). Then, we have \(B_{i,j}=^t\!F(i) \times G(j)\).

Thus, we want to find the determinant of the following matrix.

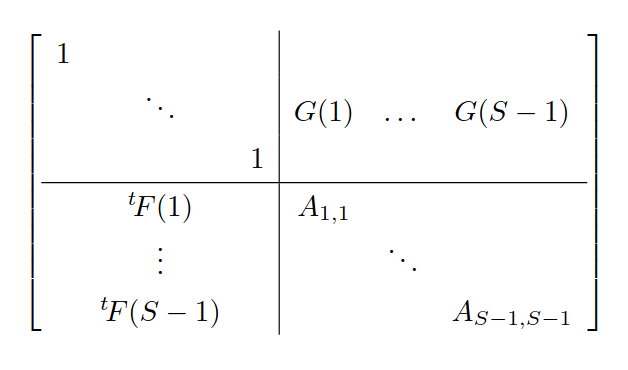
It can be seen that after sweeping the matrix from the top left, the bottom-right \((S-1) \times (S-1)\) entries will be \((A-B)\) with the \(S\)-th row and \(S\)-th column removed.

Consider sweeping this matrix from the bottom right. Then, for each \(i\) (\(1 \leq i \leq S-1\)), \(-1/A_{i,i} \times G(i) \times\ ^t\!F(i)\) will be added to the top-left \((2N-1) \times (2N-1)\) entries.

Let us find what the top-left matrix looks like in the end. The contribution of vertex \(i\) only depends on the interval written on that vertex, so let us compute the contributions for each interval altogether. By using prefix sums, the matrix can be computed in \(O(N^3)\) or \(O(N^2)\) in total.

Then, let us find the determinant of the resulted top-left matrix obediently in \(O(N^3)\).

In this way, the answer can be found in \(O(N^3)\).

Sample solution