行列木定理の知識を仮定します．

頂点数を \(S\) と置き，頂点に \(1\) から \(S\) までの番号を適当に割り当てます．

\(S\) 行 \(S\) 列の行列 \(A\) を次のように定義します．

• \(A\) は対角行列
• \(A_{i,i}=\) 頂点 \(i\) と辺で結ばれている頂点数 \(+1\)

また，\(S\) 行 \(S\) 列の行列 \(B\) を次のように定義します．

• \(B_{i,j}=\) 頂点 \(i\) と \(j\) にかかれている区間に共通部分があれば \(1\)，なければ \(0\)．特に対角成分に \(1\) が入ることに注意．

行列木定理の計算で興味があるのは \((A-B)\) という行列（の適当な行と列を除いたもの）です．

次の言い換えにより，\(B\) の見通しを良くします． 各区間 \([l,r]\) (\(1 \leq l \leq r \leq N\)) について，長さ \(2N-1\) の縦ベクトル \(F(l,r)\) および \(G(l,r)\) を以下のように定義します．

• 以下のベクトル \(v\) を \(F(l,r)\) とする
  • \(v_{2i-1}=1\) (\(i \in [l,r]\))
  • \(v_{2i-1}=0\) (\(i \not \in [l,r]\))
  • \(v_{2i}=1\) (\([i,i+1] \subset [l,r]\))
  • \(v_{2i}=0\) (\([i,i+1] \not \subset [l,r]\))
• 以下のベクトル \(v\) を \(G(l,r)\) とする
  • \(v_{2i-1}=1\) (\(i \in [l,r]\))
  • \(v_{2i-1}=0\) (\(i \not \in [l,r]\))
  • \(v_{2i}=-1\) (\([i,i+1] \subset [l,r]\))
  • \(v_{2i}=0\) (\([i,i+1] \not \subset [l,r]\))

頂点 \(i\) にかかれている区間に対応する \(F,G\) の値を，単に \(F(i),G(i)\) と書くことにします． すると，\(B_{i,j}=^t\!F(i) \times G(j)\) となります．

よって，以下の行列の行列式が求められればよいです．

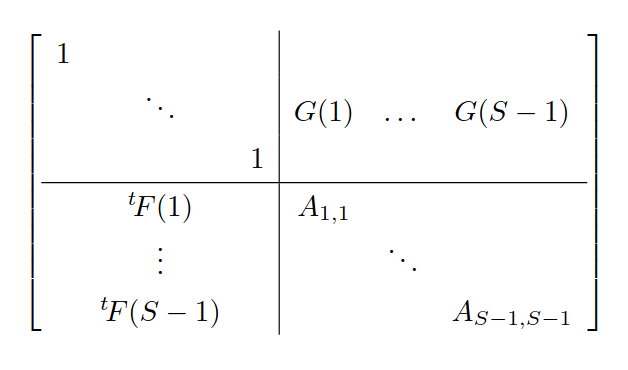
行列を左上から掃き出してゆくと，右下の \((S-1) \times (S-1)\) 成分に \((A-B)\) の \(S\) 行目と \(S\) 列目を除いたものが現れることが確認できます．

この行列を，右下から掃き出すことを考えます． すると，各 \(i\) (\(1 \leq i \leq S-1\))について，\(-1/A_{i,i} \times G(i) \times\ ^t\!F(i)\) を左上の \((2N-1) \times (2N-1)\) 成分に足すことになります．

最終的な左上行列の様子を求めます． 頂点 \(i\) の寄与は頂点 \(i\) に書かれている区間にのみ依存するので，各区間ごとに寄与をまとめて計算します． 累積和を用いることで，全体で \(O(N^3)\) or \(O(N^2)\) で行列が計算できます．

こうして得られる左上行列の行列式は，素直に \(O(N^3)\) かけて求めることにします．

よって，全体で \(O(N^3)\) で答えを求めることができます．

解答例