単純な設定の割に（問題文の主要部分は一行です）、膨大な数のステップの考察が要求されます。コンテスト中に解いた方、おめでとうございました。

この解説では、煩雑にならないように図や例を用いますが、内容は一般的に成立します。

次の図で砂の動きを表しましょう。横方向の位置は \(1\) 秒計の片方の球の中の砂の量を表し、縦方向の位置は \(\sqrt{2}\) 秒計に対する同様のものです。

すると、例えば、問題文中で説明した測定は \(A - E - F - C\) というパスに対応します。一般的には、\(A\) から出発して、壁に「衝突」するたびに速度ベクトルを変えられます。速度ベクトルには \((-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)\) のいずれかを選べます。

この図で、どのような測定が可能でしょうか。 \(A\) から出発すると、方向を三種類から選べます。\(B\) に向かうと、\(1\) 秒後に \(B\) に到達しますが、そこは本質的には \(A\) と同じ場所です。\(C\) に向かう場合も同様です。これは、測定可能な時間に \(1\) か \(\sqrt{2}\) を足したものも必ず測定可能な時間であることを意味します。

最も興味深いのは、\(E\) に向かう場合です。この場合、次の方向の選択肢が五つあります。そのうち二つでは、\(B\) か \(C\) に向かい、角に着きます。\(E\) の反対側に向かう選択肢もありますが（点線）、反対側は \(E\) と本質的に同じ場所で、測定時間に \(1\) を足すだけであるためこの移動は無視できます。残る二つの選択肢では、\(A\) か \(F\) に向かい、「斜め」の折れ線に乗り続けます。

一般的には、\(A - E - F - G - H - I - J - K - L - M - \cdots\) という斜めの折れ線があり、この上を \(A\) を出発してから前後に移動し、最後に角へ行くことになります。

この折れ線を次のように「展開」してみましょう。

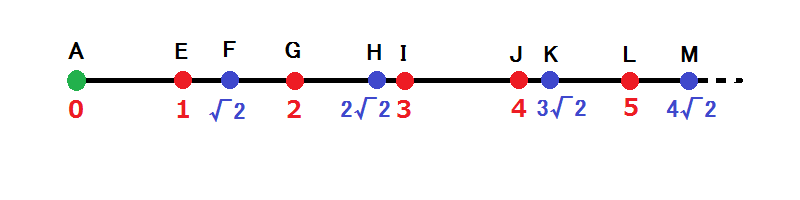
すると、測定は次のように表現できます。出発点はこの数直線上の \(A\) です。この線上では前後への移動が可能で、点に到達すると「出来事」が発生し、方向転換か \(A\) へのジャンプが可能です。

（補足: 例えば \(A - E - F - G\) や \(A - E - F - E\) の直後に \(A\) にジャンプすることはできませんが、\(A - E - F - D\) や \(A - E - F - C\) も同じ長さで、これらを代用できます。）

この数直線上でのウォークの長さとしてどのようなものがあり得るでしょうか。例として、以下の図に \(A - G - E - I - H - M - L - M - J\) を示します。

これは、\(A - M - J\) と偶数個の短い線分に分解できます。ジャンプを挟む場合も同様です。

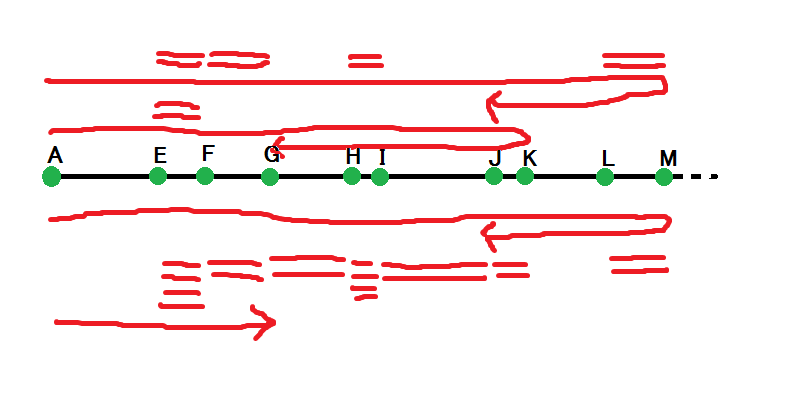
すなわち、可能な測定は必ず \(A - ? - ?\) と偶数個の短い線分と \(1\) や \(\sqrt{2}\) の倍数の和に分割できます。

厳密には、\(T\) が測定可能なのは \(T\) が以下のように表せるときです。 ここで、\(z_0, z_1, z_2, z_3, \cdots = 0, 1, \sqrt{2}, 2, \cdots\) は \(1\) の倍数と \(\sqrt{2}\) の倍数の全てを昇順に並べたものです。

\(T = 2 z_q - z_p +2 \{ \sum_{i=0}^{q-1} c_i (z_{i+1} - z_i) \} + r + s \sqrt{2}\)

\(0 \leq p \leq q, 0 \leq r\), \(0 \leq s\), \(0 \leq c_i\) は何らかの整数係数です。\(z_q\) は最も遠い到達地点に、\(z_p\) は測定終了地点に、シグマの部分は短い線分を集めたものに対応します。

次に、シグマの部分について考えましょう。\(q\) を固定したとき、この部分はどのような値をとり得るでしょうか。例えば、\(z_q = M\) のときは、\(A\) と \(M\) の間の何個かの部分区間の長さの和として表せる値を考えています。

以下の図で、点 \((x, y)\) は値 \(x + y \sqrt {2}\) に対応します。斜めの緑の直線は \(x + y \sqrt{2} = 0\)、残り二本の緑の直線は \(x = z_q, y \sqrt {2} = z_q\) です。赤い点は、一個の部分区間の長さとしてあり得る値を表します。何個かの赤い点の和になり得るのはどのような値でしょうか。

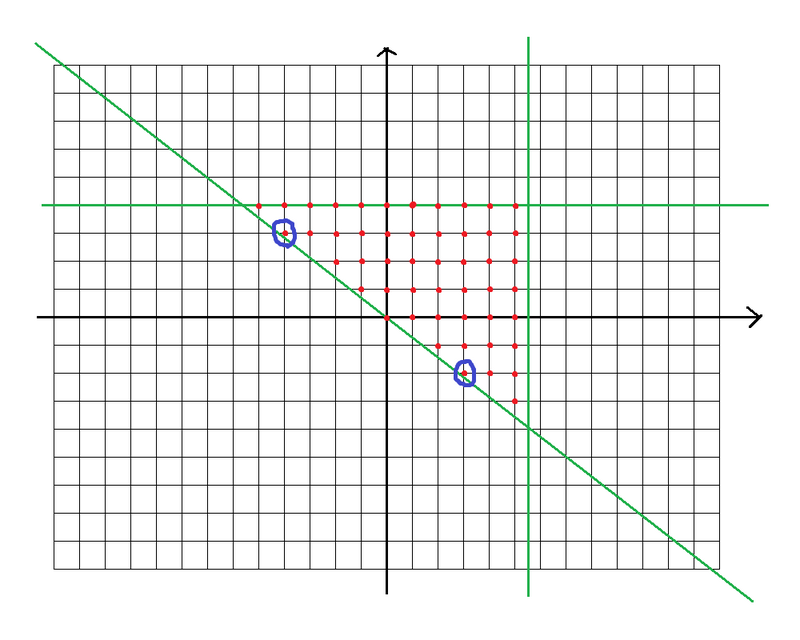
実は、青丸で囲んだ二点、すなわち原点からの傾きが最大である点が重要であることがわかります。原点から青い点のそれぞれに半直線を引くと、それら二本の半直線の上側の領域が表現可能な領域となります。例えば、次の図で、赤い点 \((-10, 8)\) は青い点の \(2\) 倍に \((-2, 2)\) を足すことで表せます（同様の方針で、「可能」領域内の全ての点を必ず表せます）。

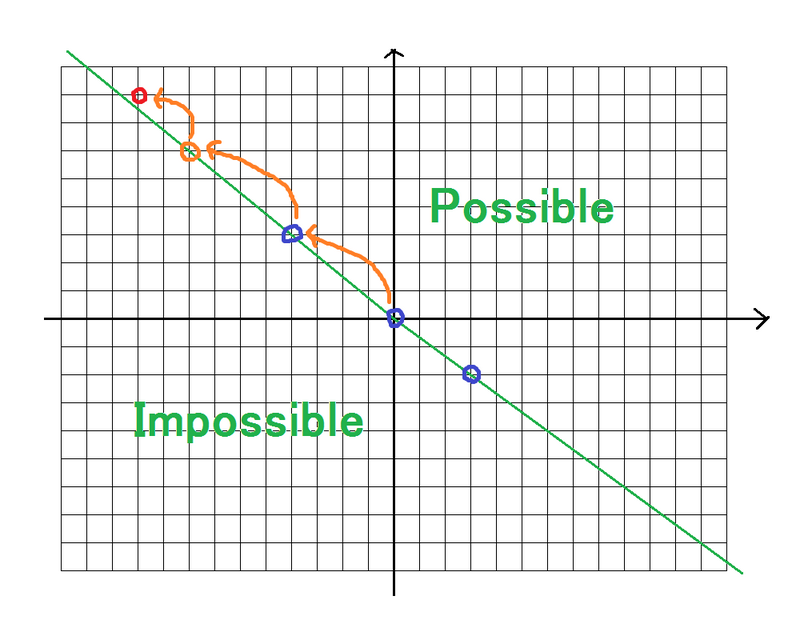
元の問題に戻りましょう。与えられた \(T\) に対して、次の表現が存在するでしょうか。

\(T = 2 z_q - z_p +2 \{ \sum_{i=0}^{q-1} c_i (z_{i+1} - z_i) \} + r + s \sqrt{2}\)

遅い解法は次の通りです。 \(z_p, z_q\) の候補を全て試し、固定しましょう。そして、もし \(T - (2 z_q - z_p)\) の座標が偶数でなければ、\(r + s \sqrt{2}\) の部分を使って調整します。その後、残りの値が上記の領域に含まれるか確かめます。

これを速くするには、「可能領域」が \(z_q\) に依存するものの、あまり頻繁には変化しないことに着目します。\(z_q\) の増加に伴って領域がどのように変化するかに注目しましょう。変化が起こるのは傾きの最大値が更新されたときのみで、それは次の \(O(\log MAX)\) 回しかありません。\(z_q = -1 + \sqrt{2}, 2 - \sqrt{2}, 3 - 2 \sqrt{2}, \cdots\) のとき、あるいは座標で表現すると、左上象限では \((-1, 1), (-4, 3), (-7, 5), (-24, 17), \cdots\) において、右下象限では \((2, -1), (3, -2), (10, -7), (17, -12), (58, -41), \dots\) においてです。

これらの座標は何なのかというと、以下の \(\sqrt{2}\) の近似列に対応します。

• \(\frac{1}{1}, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \cdots, \frac{y}{x}, \frac{2x+y}{x+y}, \cdots\)

これらの点が極点であることを厳密に示すには、例えば、三点 \((0, 0) ,(17, -12), (58, -41)\) を結ぶ三角形の面積が \(1/2\) である（したがってこれらの極点を結ぶ折れ線の下側に格子点は存在しない）ことを確かめれば十分で、いくらか計算は必要なものの単純です。

ついに、解法が得られました。 \(z_q\) と \(z_p\) を固定する代わりに、領域を固定します。 この候補は \(O(\log MAX)\) 通りしか存在しません。 固定された領域に対して、考慮する必要のある \((z_p, z_q)\) の候補は以下の二通りしかないことがわかります。

• \(z_q\) は固定された領域を実現する最小の値で、\(z_p\) は \(0\)［訳注：意図された内容はおそらく「\(z_q - z_p\) は \(0\)」］。
• \(z_q\) は固定された領域を実現する最小の値で、\(z_p\) は \(z_q\) と「種類」が異なる点のうち \(z_q\) の左側にあって \(z_q\) に最も近いもの（例えば、\(z_q = 4\) に対しては、\(3\) は種類が同じであるため \(z_p = 2 \sqrt {2}\)）。

この部分の証明も、いくらか計算は必要なものの単純です。

以上の解法は、全体でクエリあたり \(O(\log MAX)\) 時間で動作します。