 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 700 点
問題文
イカはグラフの頂点に色を塗るのが好きです。
1 から N までの番号がついた N 個の頂点と M 本の辺からなる単純無向グラフが与えられます。 全ての頂点ははじめ、色 0 で塗られています。i 番目の辺は頂点 a_i と頂点 b_i を双方向につなぐ長さ 1 の辺です。
イカはこのグラフに対して Q 回の操作を行いました。 i 回目の操作では、頂点 v_i から距離 d_i 以内にあるような頂点たち全ての色を色 c_i で上書きしました。
Q 回の操作後において、各頂点がどの色で塗られているか調べてください。
制約
- 1 ≦ N,M,Q ≦ 10^5
- 1 ≦ a_i,b_i,v_i ≦ N
- a_i ≠ b_i
- 0 ≦ d_i ≦ 10
- 1 ≦ c_i ≦10^5
- d_i, c_i いずれも整数
- 与えられるグラフに自己ループや多重辺は存在しない
部分点
- 1 ≦ N,M,Q ≦ 2{,}000 を満たすデータセットに正解した場合は、部分点として 200 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N M
a_1 b_1
:
a_{M} b_{M}
Q
v_1 d_1 c_1
:
v_{Q} d_{Q} c_{Q}
出力
答えを N 行に出力せよ。 i 行目では Q 回の操作後における頂点 i の色を出力せよ。
入力例 1
7 7 1 2 1 3 1 4 4 5 5 6 5 7 2 3 2 6 1 1 1 2 2
出力例 1
2 2 2 2 2 1 0
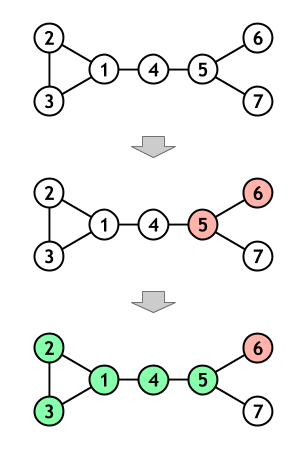
はじめ、各頂点は色 0 で塗られています。 1 回目の操作により、頂点 5,6 が色 1 で塗られます。 2 回目の操作により、頂点 1,2,3,4,5 が色 2 で塗られます。
入力例 2
14 10 1 4 5 7 7 11 4 10 14 7 14 3 6 14 8 11 5 13 8 3 8 8 6 2 9 7 85 6 9 3 6 7 5 10 3 1 12 9 4 9 6 6 8 2 3
出力例 2
1 0 3 1 5 5 3 3 6 1 3 4 5 3
与えられるグラフは連結とは限りません。
Score : 700 points
Problem Statement
Squid loves painting vertices in graphs.
There is a simple undirected graph consisting of N vertices numbered 1 through N, and M edges. Initially, all the vertices are painted in color 0. The i-th edge bidirectionally connects two vertices a_i and b_i. The length of every edge is 1.
Squid performed Q operations on this graph. In the i-th operation, he repaints all the vertices within a distance of d_i from vertex v_i, in color c_i.
Find the color of each vertex after the Q operations.
Constraints
- 1 ≤ N,M,Q ≤ 10^5
- 1 ≤ a_i,b_i,v_i ≤ N
- a_i ≠ b_i
- 0 ≤ d_i ≤ 10
- 1 ≤ c_i ≤10^5
- d_i and c_i are all integers.
- There are no self-loops or multiple edges in the given graph.
Partial Score
- 200 points will be awarded for passing the testset satisfying 1 ≤ N,M,Q ≤ 2{,}000.
Input
Input is given from Standard Input in the following format:
N M
a_1 b_1
:
a_{M} b_{M}
Q
v_1 d_1 c_1
:
v_{Q} d_{Q} c_{Q}
Output
Print the answer in N lines. In the i-th line, print the color of vertex i after the Q operations.
Sample Input 1
7 7 1 2 1 3 1 4 4 5 5 6 5 7 2 3 2 6 1 1 1 2 2
Sample Output 1
2 2 2 2 2 1 0
Initially, each vertex is painted in color 0. In the first operation, vertices 5 and 6 are repainted in color 1. In the second operation, vertices 1, 2, 3, 4 and 5 are repainted in color 2.

Sample Input 2
14 10 1 4 5 7 7 11 4 10 14 7 14 3 6 14 8 11 5 13 8 3 8 8 6 2 9 7 85 6 9 3 6 7 5 10 3 1 12 9 4 9 6 6 8 2 3
Sample Output 2
1 0 3 1 5 5 3 3 6 1 3 4 5 3
The given graph may not be connected.