 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 800 点
問題文
高橋君は,N 頂点 1, 2, ..., N からなる無向グラフをもらいました. このグラフの辺は (u_i, v_i) で表されます. このグラフには,自己辺や多重辺は存在しません.
高橋君は,このグラフをもとに,N^2 頂点 (a, b) (1 \leq a \leq N, 1 \leq b \leq N) からなるグラフを作ることにしました. このグラフの辺は,次の規則で定まります.
- 元のグラフにおいて a と a' の間および b と b' の間の両方に辺があるとき,またそのときに限り,(a, b) と (a', b') の間に辺を張る.
このようにして作ったグラフの連結成分の個数を求めてください.
制約
- 2 \leq N \leq 100,000
- 0 \leq M \leq 200,000
- 1 \leq u_i < v_i \leq N
- u_i = u_j かつ v_i = v_j を満たすような異なる i, j の組は存在しない
入力
入力は以下の形式で標準入力から与えられる。
N M u_1 v_1 u_2 v_2 : u_M v_M
出力
高橋君の作ったグラフの連結成分の個数を出力せよ.
入力例 1
3 1 1 2
出力例 1
7
高橋君の作ったグラフは下のようになります.
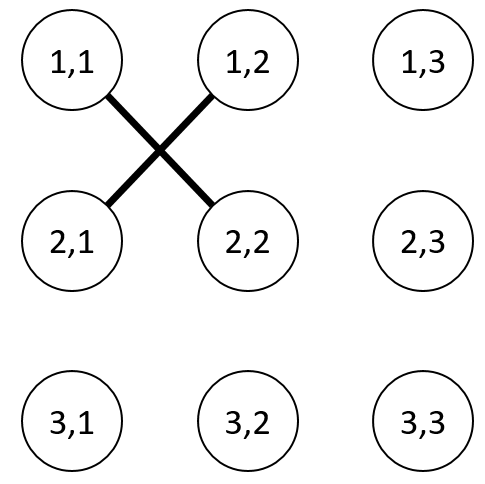
入力例 2
7 5 1 2 3 4 3 5 4 5 2 6
出力例 2
18
Score : 800 points
Problem Statement
Takahashi has received an undirected graph with N vertices, numbered 1, 2, ..., N. The edges in this graph are represented by (u_i, v_i). There are no self-loops and multiple edges in this graph.
Based on this graph, Takahashi is now constructing a new graph with N^2 vertices, where each vertex is labeled with a pair of integers (a, b) (1 \leq a \leq N, 1 \leq b \leq N). The edges in this new graph are generated by the following rule:
- Span an edge between vertices (a, b) and (a', b') if and only if both of the following two edges exist in the original graph: an edge between vertices a and a', and an edge between vertices b and b'.
How many connected components are there in this new graph?
Constraints
- 2 \leq N \leq 100,000
- 0 \leq M \leq 200,000
- 1 \leq u_i < v_i \leq N
- There exists no pair of distinct integers i and j such that u_i = u_j and v_i = v_j.
Input
The input is given from Standard Input in the following format:
N M u_1 v_1 u_2 v_2 : u_M v_M
Output
Print the number of the connected components in the graph constructed by Takahashi.
Sample Input 1
3 1 1 2
Sample Output 1
7
The graph constructed by Takahashi is as follows.

Sample Input 2
7 5 1 2 3 4 3 5 4 5 2 6
Sample Output 2
18