 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 800 点
問題文
N 人の人が大会に出場しました。この大会はトーナメント形式であり、N-1 回の試合が行われました。 諸事情により、このトーナメントは全参加者に平等に組まれているとは限りません。 すなわち、各人に対し、優勝するために必要なその人が勝者となるような試合数が等しいとは限りません。 トーナメントの構造は、正式には問題文の末尾で定義されます。
各試合では必ず片方の人が勝者、もう片方の人が敗者となり、最後まで負けなかった 1 人が優勝となります。
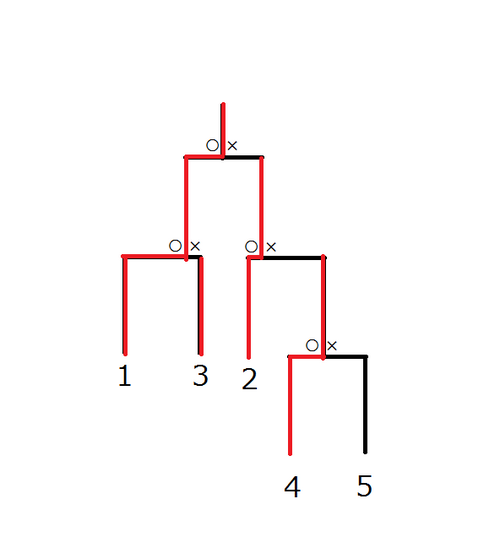
図: トーナメントの例
人には 1 から N までの番号がついており、1 番の人が優勝し、優勝者以外の人 i(2 ≦ i ≦ N) は人 a_i との試合で負けました。
トーナメントの深さとは、すべての人に対する、その人が優勝するために必要な、その人が勝者となるような試合数の最大値です。
トーナメントの深さとしてありうる最小の値を求めてください。
トーナメントの構造の正式な定義は以下の通りです。i 回目の試合では、
- あらかじめ決められた、まだ試合をしていない 2 人の人
- あらかじめ決められたまだ試合をしていない人 1 人と、あらかじめ決められた j(j<i) に対する、j 回目の試合の勝者
- あらかじめ決められた j,k(j,k<i, j ≠ k) に対する、j 回目の試合の勝者と k 回目の試合の勝者
のうちのいずれかの 2 人が試合を行います。このような構造であって、どのように試合結果を決めても、すでに一度試合に負けた人が再び試合をすることのないようなものをトーナメントと呼びます。
制約
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i ≦ N(2 ≦ i ≦ N)
- 入力の試合結果と合致するようなトーナメントが存在する
入力
入力は以下の形式で標準入力から与えられる。
N a_2 : a_N
出力
トーナメントの深さとしてありうる最小の値を出力せよ。
入力例 1
5 1 1 2 4
出力例 1
3
次のような試合結果が条件を満たします。
- 1 回目の試合では、人 4 と 人 5 が対戦し、人 4 が勝つ
- 2 回目の試合では、人 2 と 人 4 が対戦し、人 2 が勝つ
- 3 回目の試合では、人 1 と 人 3 が対戦し、人 1 が勝つ
- 4 回目の試合では、人 1 と 人 2 が対戦し、人 1 が勝つ

このトーナメントは、人 5 が優勝するためには 3 回勝利する必要があるので、深さ 3 のトーナメントとなります。 逆に、深さ 2 以下の条件を満たすトーナメントは存在しないので、3 を出力します。
入力例 2
7 1 2 1 3 1 4
出力例 2
3
入力例 3
4 4 4 1
出力例 3
3
Score : 800 points
Problem Statement
N contestants participated in a competition. The total of N-1 matches were played in a knockout tournament. For some reasons, the tournament may not be "fair" for all the contestants. That is, the number of the matches that must be played in order to win the championship may be different for each contestant. The structure of the tournament is formally described at the end of this statement.
After each match, there were always one winner and one loser. The last contestant standing was declared the champion.

Figure: an example of a tournament
For convenience, the contestants were numbered 1 through N. The contestant numbered 1 was the champion, and the contestant numbered i(2 ≦ i ≦ N) was defeated in a match against the contestant numbered a_i.
We will define the depth of the tournament as the maximum number of the matches that must be played in order to win the championship over all the contestants.
Find the minimum possible depth of the tournament.
The formal description of the structure of the tournament is as follows. In the i-th match, one of the following played against each other:
- Two predetermined contestants
- One predetermined contestant and the winner of the j-th match, where j(j<i) was predetermined
- The winner of the j-th match and the winner of the k-th match, where j and k (j,k<i, j ≠ k) were predetermined
Such structure is valid structure of the tournament, if and only if no contestant who has already been defeated in a match will never play in a match, regardless of the outcome of the matches.
Constraints
- 2 ≦ N ≦ 10^5
- 1 ≦ a_i ≦ N(2 ≦ i ≦ N)
- It is guaranteed that the input is consistent (that is, there exists at least one tournament that matches the given information).
Input
The input is given from Standard Input in the following format:
N a_2 : a_N
Output
Print the minimum possible depth of the tournament.
Sample Input 1
5 1 1 2 4
Sample Output 1
3
The following tournament and the result of the matches are consistent with the given information:
- In the first match, contestants 4 and 5 played against each other, and contestant 4 won.
- In the second match, contestants 2 and 4 played against each other, and contestant 2 won.
- In the third match, contestants 1 and 3 played against each other, and contestant 1 won.
- In the fourth match, contestants 1 and 2 played against each other, and contestant 1 won.

The depth of this tournament is 3, since contestant 5 must play three matches in order to win the championship. There is no tournament with depth 2 or less that is consistent with the given information, thus the output should be 3.
Sample Input 2
7 1 2 1 3 1 4
Sample Output 2
3
Sample Input 3
4 4 4 1
Sample Output 3
3