/ 
Time Limit: 5 sec / Memory Limit: 512 MB
配点 : 1900 点
問題文
高橋君はある日青木君から以下の様な問題を貰いました。
- N 頂点の木と、整数 K が与えられる。木の頂点は 1,2,...,N と番号がついているものとし、辺は (a_i, b_i) で表す。
- 頂点の集合 S について f(S) を、S をすべて含む部分木の頂点数の最小値とする
- 木から K 個の頂点を選ぶ方法は _NC_K 通りあるが、それぞれについて選んだ頂点を S とし、 f(S) の総和を求める
- 答えは大きくなることがあるので、924844033(素数) で割ったあまりを出力する
高橋君にとってこの問題は簡単すぎました。なので K = 1,2,...,N 全てについてこの問題を解くことにしました。
制約
- 2 ≦ N ≦ 200,000
- 1 ≦ a_i, b_i ≦ N
- 与えられるグラフは木である
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
出力
N 行出力する。i 行目には、K=i の時の問題の答えを 924844033 で割ったあまりを出力する。
入力例 1
3 1 2 2 3
出力例 1
3 7 3
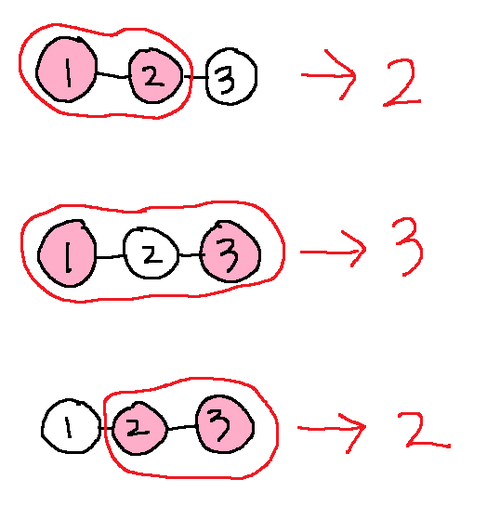
上図は、K=2 の場合を図示している。ピンク色の頂点が選んだ頂点で、赤く囲われたのが頂点数最小の部分木である。
入力例 2
4 1 2 1 3 1 4
出力例 2
4 15 13 4
入力例 3
7 1 2 2 3 2 4 4 5 4 6 6 7
出力例 3
7 67 150 179 122 45 7
Score : 1900 points
Problem Statement
One day, Takahashi was given the following problem from Aoki:
- You are given a tree with N vertices and an integer K. The vertices are numbered 1 through N. The edges are represented by pairs of integers (a_i, b_i).
- For a set S of vertices in the tree, let f(S) be the minimum number of the vertices in a subtree of the given tree that contains all vertices in S.
- There are
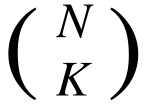ways to choose K vertices from the trees. For each of them, let S be the set of the chosen vertices, and find the sum of f(S) over all 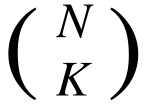ways. - Since the answer may be extremely large, print it modulo 924844033(prime).
Since it was too easy for him, he decided to solve this problem for all K = 1,2,...,N.
Constraints
- 2 ≦ N ≦ 200,000
- 1 ≦ a_i, b_i ≦ N
- The given graph is a tree.
Input
The input is given from Standard Input in the following format:
N
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
Output
Print N lines. The i-th line should contain the answer to the problem where K=i, modulo 924844033.
Sample Input 1
3 1 2 2 3
Sample Output 1
3 7 3
The diagram above illustrates the case where K=2. The chosen vertices are colored pink, and the subtrees with the minimum number of vertices are enclosed by red lines.
Sample Input 2
4 1 2 1 3 1 4
Sample Output 2
4 15 13 4
Sample Input 3
7 1 2 2 3 2 4 4 5 4 6 6 7
Sample Output 3
7 67 150 179 122 45 7