 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1400 点
問題文
しぐま君とすぎむ君はゲームをすることにしました。
このゲームは N 頂点のグラフの上で行います。頂点には 1,2,...,N と番号がついています。グラフには N-1 本の赤い辺と N-1 本の青い辺があり、どちらも木となっています。赤い辺は (a_i, b_i) で表し、青い辺は (c_i, d_i) で表します。
二人はそれぞれ駒を 1 個ずつ持っており、しぐま君の駒の初期位置は頂点 X、すぎむ君の駒の初期位置は頂点 Y です。
このゲームはターン制で、ターン 1, ターン 2, ターン 3, ... と進んでいきます。そして、ターン 1, 3, 5, ... はしぐま君、ターン 2, 4, 6, ... はすぎむ君の手番です。
二人は自分の手番では、自分の駒を動かすかパスをします。ただし動かせる頂点には制限があり、しぐま君は赤い辺、すぎむ君は青い辺で隣り合った頂点のみに駒を動かせます。
もし二つの駒が同じ頂点に来るとその時点でゲームは終了します。そしてターン i での操作の後にゲームが終了したならば、i を総ターン数とします。
しぐま君は総ターン数を出来る限り大きく、すぎむ君は出来る限り小さくしたいです。
二人はこの目的のもとで最適に行動をすると仮定したとき、ゲームは終了するかを判定し、終了する場合は総ターン数はいくつになるか求めてください。
制約
- 2 ≦ N ≦ 200,000
- 1 ≦ X, Y ≦ N
- X \neq Y
- 1 ≦ a_i, b_i, c_i, d_i ≦ N
- 赤い辺と青い辺はそれぞれ木である
入力
入力は以下の形式で標準入力から与えられる。
N X Y
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
c_1 d_1
c_2 d_2
:
c_{N-1} d_{N-1}
出力
1 行に答えを出力する。
ただし、いつまでもゲームが終了しない場合は -1 を出力する。
入力例 1
4 1 2 1 2 1 3 1 4 2 1 2 3 1 4
出力例 1
4
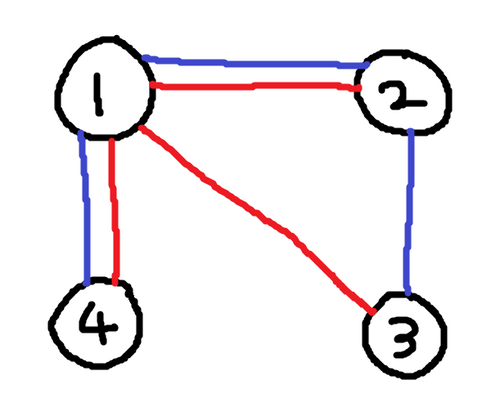
入力例 2
3 3 1 1 2 2 3 1 2 2 3
出力例 2
4
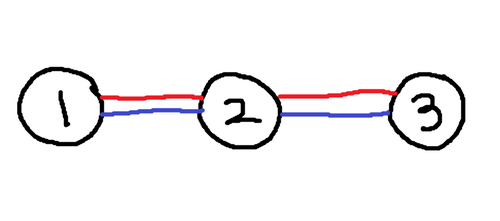
入力例 3
4 1 2 1 2 3 4 2 4 1 2 3 4 1 3
出力例 3
2
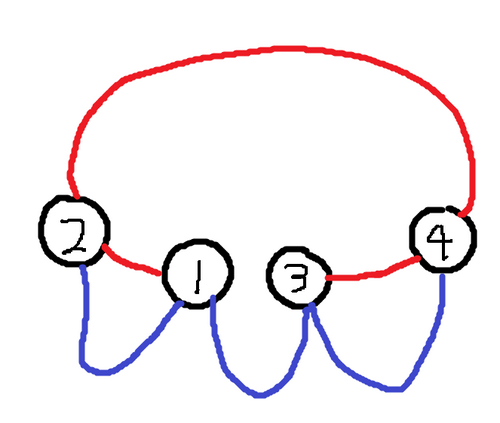
入力例 4
4 2 1 1 2 3 4 2 4 1 2 3 4 1 3
出力例 4
-1
入力例 5
5 1 2 1 2 1 3 1 4 4 5 2 1 1 3 1 5 5 4
出力例 5
6
Score : 1400 points
Problem Statement
Sigma and Sugim are playing a game.
The game is played on a graph with N vertices numbered 1 through N. The graph has N-1 red edges and N-1 blue edges, and the N-1 edges in each color forms a tree. The red edges are represented by pairs of integers (a_i, b_i), and the blue edges are represented by pairs of integers (c_i, d_i).
Each player has his own piece. Initially, Sigma's piece is at vertex X, and Sugim's piece is at vertex Y.
The game is played in turns, where turns are numbered starting from turn 1. Sigma takes turns 1, 3, 5, ..., and Sugim takes turns 2, 4, 6, ....
In each turn, the current player either moves his piece, or does nothing. Here, Sigma can only move his piece to a vertex that is directly connected to the current vertex by a red edge. Similarly, Sugim can only move his piece to a vertex that is directly connected to the current vertex by a blue edge.
When the two pieces come to the same vertex, the game ends immediately. If the game ends just after the operation in turn i, let i be the total number of turns in the game.
Sigma's objective is to make the total number of turns as large as possible, while Sugim's objective is to make it as small as possible.
Determine whether the game will end in a finite number of turns, assuming both players plays optimally to achieve their respective objectives. If the answer is positive, find the number of turns in the game.
Constraints
- 2 ≦ N ≦ 200,000
- 1 ≦ X, Y ≦ N
- X \neq Y
- 1 ≦ a_i, b_i, c_i, d_i ≦ N
- The N-1 edges in each color (red and blue) forms a tree.
Input
The input is given from Standard Input in the following format:
N X Y
a_1 b_1
a_2 b_2
:
a_{N-1} b_{N-1}
c_1 d_1
c_2 d_2
:
c_{N-1} d_{N-1}
Output
If the game will end in a finite number of turns, print the number of turns.
Otherwise, print -1.
Sample Input 1
4 1 2 1 2 1 3 1 4 2 1 2 3 1 4
Sample Output 1
4

Sample Input 2
3 3 1 1 2 2 3 1 2 2 3
Sample Output 2
4

Sample Input 3
4 1 2 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 3
2

Sample Input 4
4 2 1 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 4
-1
Sample Input 5
5 1 2 1 2 1 3 1 4 4 5 2 1 1 3 1 5 5 4
Sample Output 5
6