 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 600 点
問題文
N 頂点の木があり、頂点には 1 ~ N の番号がついています。N - 1 本の辺について、i (1≦i≦N-1) 本目の辺は頂点 A_i と頂点 B_i を繋いでいます。
この木の直径を K 以下にするために削除する必要のある頂点数の最小値を求めてください。 ただし、頂点を削除した後のグラフは連結になっていなければなりません。
木の直径とは、2 つの頂点間の距離の最大値のことを指します。2 つの頂点間の距離とは、2 つの頂点を結ぶパスに含まれる辺の本数を指します。
制約
- 2≦N≦2000
- 1≦K≦N-1
- 1≦A_i≦N, 1≦B_i≦N
- 与えられるグラフは木である。
入力
入力は以下の形式で標準入力から与えられる。
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
出力
直径を K 以下にするために削除する必要のある頂点数の最小値を出力せよ。
入力例 1
6 2 1 2 3 2 4 2 1 6 5 6
出力例 1
2
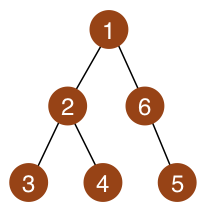
木の構造は図のとおりです。 頂点 5,6 を削除すると直径を 2 に出来ます。
入力例 2
6 5 1 2 3 2 4 2 1 6 5 6
出力例 2
0
すでに直径が K 以下なので、頂点を削除する必要はありません。
Score : 600 points
Problem Statement
Given an undirected tree, let the distance between vertices u and v be the number of edges on the simple path from u to v. The diameter of a tree is the maximum among the distances between any two vertices. We will call a tree good if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting tree is good. When a vertex is removed, all incident edges will also be removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to produce a good tree.
Constraints
- 2≦N≦2000
- 1≦K≦N-1
- 1≦A_i≦N, 1≦B_i≦N
- The graph defined by A_i and B_i is a tree.
Input
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
Output
Print the minimum number of vertices that you need to remove in order to produce a good tree.
Sample Input 1
6 2 1 2 3 2 4 2 1 6 5 6
Sample Output 1
2
The tree is shown below. Removing vertices 5 and 6 will result in a good tree with the diameter of 2.

Sample Input 2
6 5 1 2 3 2 4 2 1 6 5 6
Sample Output 2
0
Since the given tree is already good, you do not need to remove any vertex.