E - Cycle Graph? Editorial /

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 300 点

問題文

N 頂点 M 辺の単純無向グラフが与えられます。頂点には 1,2,\dots,N の番号が、辺には 1,2,\dots,M の番号がつけられており、辺 i は頂点 A_i と頂点 B_i を結んでいます。

このグラフがサイクルグラフであるか判定してください。

単純無向グラフとは 単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。

サイクルグラフとは 頂点に 1, 2, \dots, N の番号が付けられた N 頂点のグラフがサイクルグラフであるとは、(1, 2, \dots, N) を並べ変えて得られる数列 (v_1, v_2, \dots, v_N) であって、以下の条件を満たすものが存在することをいいます。
  • i = 1, 2, \dots, N-1 に対して、頂点 v_i と v_{i+1} を結ぶ辺が存在する
  • 頂点 v_N と v_1 を結ぶ辺が存在する
  • それら以外の辺は存在しない

制約

  • 3\leq N \leq 2\times 10^5
  • 0 \leq M \leq 2\times 10^5
  • 1 \leq A_i, B_i \leq N
  • 与えられるグラフは単純
  • 入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1
\vdots
A_M B_M

出力

与えられたグラフがサイクルグラフであるなら Yes、そうでないなら No と出力せよ。

入力例 1

4 4
2 4
3 1
4 1
2 3

出力例 1

Yes

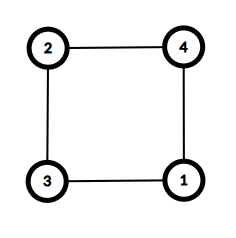
与えられたグラフは以下の通りであり、これはサイクルグラフです。

図

入力例 2

4 6
1 2
1 3
1 4
2 3
2 4
3 4

出力例 2

No

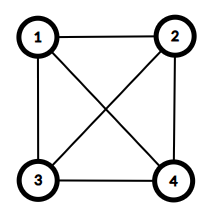
与えられたグラフは以下の通りであり、これはサイクルグラフではありません。

図

Score : 300 points

Problem Statement

You are given a simple undirected graph with N vertices and M edges. The vertices are numbered 1,2,\dots,N and the edges are numbered 1,2,\dots,M. Edge i connects vertices A_i and B_i.

Determine whether this graph is a cycle graph.

Definition of simple undirected graph A simple undirected graph is a graph with undirected edges without self-loops or multi-edges.

Definition of cycle graph An N-vertex graph with vertices labeled 1,2,\dots,N is a cycle graph when there exists a permutation (v_1,v_2,\dots,v_N) of (1,2,\dots,N) such that:
  • For each i = 1,2,\dots,N-1, there is an edge between vertices v_i and v_{i+1}.
  • There is an edge between vertices v_N and v_1.
  • No other edges exist.

Constraints

  • 3 \le N \le 2\times 10^5
  • 0 \le M \le 2\times 10^5
  • 1 \le A_i, B_i \le N
  • The given graph is simple.
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1
\vdots
A_M B_M

Output

Output Yes if the given graph is a cycle graph; otherwise, print No.

Sample Input 1

4 4
2 4
3 1
4 1
2 3

Sample Output 1

Yes

The given graph is as follows, and this is a cycle graph.

Figure

Sample Input 2

4 6
1 2
1 3
1 4
2 3
2 4
3 4

Sample Output 2

No

The given graph is as follows, and this is not a cycle graph.

Figure