この問題で入力されるグラフは Functional Graph と呼ばれるグラフです。Functional Graph は少なくない頻度で出題されるテーマなので、グラフの特徴を押さえておきましょう。
Functional Graph の性質として次の性質が挙げられます。

Functional Graph の性質

\(G\) の連結成分が \(K\) 個あって \(C_1, C_2, \dots, C_K\) とする。このとき、各連結成分には閉路が \(1\) つだけ存在する。

証明は ABC256 E の解説 に詳しく書かれています。

この性質を利用して今回の問題を解きましょう。まず、各連結成分ごとに独立に問題を解くことを考えます。各連結成分は次の図のように、1 個の閉路があり、その閉路に有向木がくっついた形をしています。

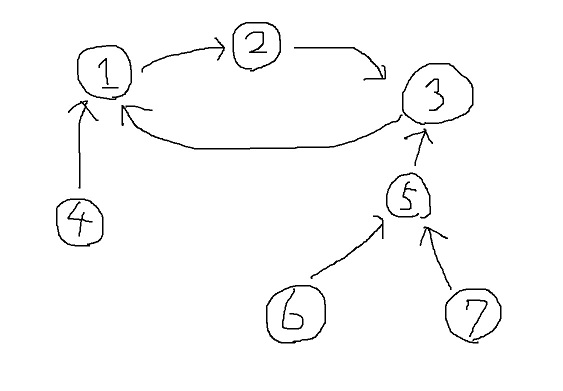
例えば、図のいくつかの頂点において、その頂点から到達可能な頂点を列挙してみると次のようになります。

• 頂点 \(1\) から到達可能な頂点は頂点 \(1, 2, 3\) である。
• 頂点 \(4\) から到達可能な頂点は頂点 \(1, 2, 3, 4\) である。
• 頂点 \(7\) から到達可能な頂点は頂点 \(1,2,3,5,7\) である。

この性質を一般化すると、次の事実が分かります。(証明は省略します。)

頂点 \(u\) から到達可能な頂点は次の 2 種類であり、かつそれらによって尽くされる。

• 頂点 \(u\) を含む有向木における \(u\) の祖先である頂点
• 頂点 \(u\) を含む有向木の根を含む閉路に含まれる頂点

このような性質が分かれば、あとは DFS などのグラフ探索アルゴリズムを用いて、各頂点 \(u\) について

• 頂点 \(u\) を含む有向木における \(u\) の深さ
• 頂点 \(u\) を含む有向木の根を含む閉路の頂点数

を適切に計算すればよいです。計算量は \(\mathrm{O}(N)\) 程度で十分高速です。
なお、別解として 強成分連結分解 (SCC) を利用する解法もあります。興味がある方は考えてみましょう。