 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
二次元平面上に N 体のモンスターがいます。 モンスターには 1 から N までの番号が付けられており、モンスター i がいる場所の座標は (X_i,Y_i) です。 ここで、(X_i,Y_i) \neq (0,0) です。 (なお、各モンスターは静止した点としてみなせるものとします。すなわち、モンスターは大きさを持ちません。)
この平面上の原点には高橋君が立っています。 高橋君の目からは強力なレーザーが常に照射されており、高橋君が向いている方向に存在するモンスターは即座に消滅します。 高橋君が向いている方向に複数のモンスターが存在する場合も、その全てが即座に消滅します。
青木君は、Q 個の 独立な 思考実験を行なっています。 j 個目の思考実験は以下のようなものです。
- はじめ、高橋君はモンスター A_j がいる方向を向いている。今から高橋君は 時計回り に回転を行い、モンスター B_j がいる方向を向いた瞬間に停止する。 このとき、(モンスター A_j,B_j を含め)合計で何体のモンスターが消滅するか?なお、モンスター A_j,B_j が原点から見て同じ方向に存在する場合、高橋君は一切回転しない。
各思考実験に対する答えを求めてください。
制約
- 2\leq N \leq 2\times 10^5
- 1\leq Q \leq 2\times 10^5
- -10^9\leq X_i,Y_i \leq 10^9
- (X_i,Y_i)\neq (0,0)
- 1\leq A_j,B_j\leq N
- A_j\neq B_j
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q X_1 Y_1 X_2 Y_2 \vdots X_N Y_N A_1 B_1 A_2 B_2 \vdots A_Q B_Q
出力
Q 行出力せよ。 j 行目 (1\leq j \leq Q) には、j 個目の思考実験に対する答えを出力せよ。
入力例 1
5 4 0 1 1 -2 1 0 -2 0 3 0 4 1 1 4 5 4 3 5
出力例 1
2 5 4 2
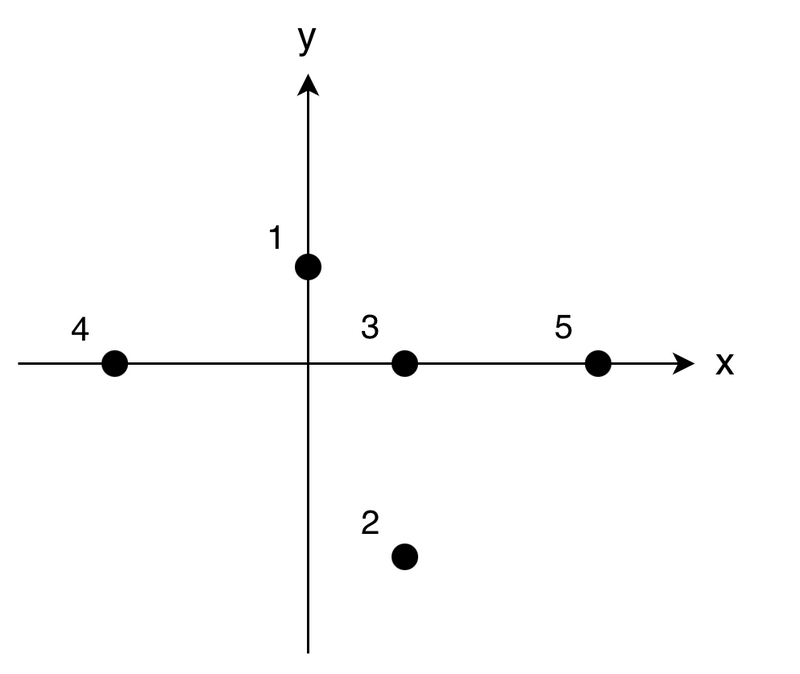
- 1 個目の思考実験:はじめ、高橋君はモンスター 4 がいる方向を向いています(このとき、モンスター 4 が消滅します)。 ここから時計回りに回転を続け、モンスター 1 がいる方向を向いた瞬間に停止します(このとき、モンスター 1 が消滅します)。 これら以外のモンスターがいる方向を向くことはないため、答えは 2 です。
- 2 個目の思考実験:はじめ、高橋君はモンスター 1 がいる方向を向いています(このとき、モンスター 1 が消滅します)。 ここから時計回りに回転を続けると、途中モンスター 3,5 がいる方向を向くため、これらが消滅します。 さらに回転を続けると、途中モンスター 2 がいる方向を向くため、これが消滅します。 最終的にモンスター 4 がいる方向を向いた瞬間に停止します(このとき、モンスター 4 が消滅します)。 よって、答えは 5 です。
- 3 個目の思考実験:モンスター 3,5,2,4 が消滅するため、答えは 4 です。
- 4 個目の思考実験:モンスター 3,5 が消滅するため、答えは 2 です。 なお、モンスター 3,5 は原点から見て同じ方向に存在するため、高橋君は一切回転しないことに注意してください。
入力例 2
2 1 1 2 1 2 1 2
出力例 2
2
同じ座標に複数のモンスターが存在することもあります。
入力例 3
8 10 -84 -60 -100 8 77 55 -14 -10 50 -4 -63 -45 26 -17 -7 -5 3 7 2 4 8 4 8 4 7 1 1 7 6 3 4 7 4 5 2 6
出力例 3
3 8 4 4 5 8 6 8 7 8
Score : 450 points
Problem Statement
There are N monsters on a two-dimensional plane. The monsters are numbered from 1 to N, and the coordinates of monster i are (X_i,Y_i). Here, (X_i,Y_i) \neq (0,0). (Each monster can be regarded as a stationary point. That is, monsters have no size.)
Takahashi is standing at the origin of this plane. A powerful laser is always emitted from his eyes, instantly destroying monsters in the direction he is facing. If multiple monsters exist in the direction he is facing, all of them are instantly destroyed.
Aoki is conducting Q independent thought experiments. The j-th thought experiment is as follows:
- Initially, Takahashi is facing the direction toward monster A_j. From now on, Takahashi will rotate clockwise and stop the moment he faces the direction toward monster B_j. Here, how many monsters in total (including monsters A_j and B_j) will be destroyed? If monsters A_j and B_j exist in the same direction from the origin, Takahashi does not rotate at all.
Find the answer to each thought experiment.
Constraints
- 2\leq N \leq 2\times 10^5
- 1\leq Q \leq 2\times 10^5
- -10^9\leq X_i,Y_i \leq 10^9
- (X_i,Y_i)\neq (0,0)
- 1\leq A_j,B_j\leq N
- A_j\neq B_j
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q X_1 Y_1 X_2 Y_2 \vdots X_N Y_N A_1 B_1 A_2 B_2 \vdots A_Q B_Q
Output
Output Q lines. The j-th line (1\leq j \leq Q) should contain the answer to the j-th thought experiment.
Sample Input 1
5 4 0 1 1 -2 1 0 -2 0 3 0 4 1 1 4 5 4 3 5
Sample Output 1
2 5 4 2

- 1-st thought experiment: Initially, Takahashi is facing the direction toward monster 4 (at this time, monster 4 is destroyed). From here, he continues to rotate clockwise and stops the moment he faces the direction toward monster 1 (at this time, monster 1 is destroyed). Since he does not face the direction toward any other monsters, the answer is 2.
- 2-nd thought experiment: Initially, Takahashi is facing the direction toward monster 1 (at this time, monster 1 is destroyed). From here, as he continues to rotate clockwise, he faces the direction toward monsters 3 and 5 along the way, so they are destroyed. As he continues to rotate further, he faces the direction toward monster 2 along the way, so it is destroyed. Finally, he stops the moment he faces the direction toward monster 4 (at this time, monster 4 is destroyed). Therefore, the answer is 5.
- 3-rd thought experiment: Monsters 3, 5, 2, 4 are destroyed, so the answer is 4.
- 4-th thought experiment: Monsters 3, 5 are destroyed, so the answer is 2. Note that since monsters 3 and 5 exist in the same direction from the origin, Takahashi does not rotate at all.
Sample Input 2
2 1 1 2 1 2 1 2
Sample Output 2
2
Multiple monsters may exist at the same coordinates.
Sample Input 3
8 10 -84 -60 -100 8 77 55 -14 -10 50 -4 -63 -45 26 -17 -7 -5 3 7 2 4 8 4 8 4 7 1 1 7 6 3 4 7 4 5 2 6
Sample Output 3
3 8 4 4 5 8 6 8 7 8