 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
無限に広がる二次元グリッドがあります。マス (x,y) の色は、0 \leq x \leq X-1 かつ 0 \leq y \leq Y-1 ならば黒であり、そうでなければ白です。
このグリッドに対して N 個の大嵐が順に発生します。i 回目の大嵐は、文字 C_i と整数 A_i, B_i で表される法則にしたがって、グリッド上の各マスの色を更新します。
i 回目の大嵐において、大嵐が起きた後のマス (x, y) の色は、
- C_i が
Xの場合、- x < A_i ならば、大嵐が起きる前のマス (x, y + B_i) の色になる。
- x \geq A_i ならば、大嵐が起きる前のマス (x, y - B_i) の色になる。
- C_i が
Yの場合、- y < A_i ならば、大嵐が起きる前のマス (x + B_i, y) の色になる。
- y \geq A_i ならば、大嵐が起きる前のマス (x - B_i, y) の色になる。
2 つの黒いマス (x_1, y_1), (x_2, y_2) が隣接しているとは、|x_1 - x_2| + |y_1 - y_2| = 1 が満たされることを指します。また、2 つの黒いマス c_1, c_2 が連結であるとは、隣接する黒いマスへの移動を繰り返すことでマス c_1 からマス c_2 に移動できることを指します。
空でない黒いマスの集合 S が連結成分であるとは、S が以下の条件を満たすことを指します。
- S に属するどの 2 マスも連結である。
- S に属さないすべての黒いマスが、S に属するどのマスとも連結でない。
N 個の大嵐がすべて発生した後のグリッドについて、連結成分の個数を求め、各連結成分におけるマスの個数を昇順に出力してください。
制約
- N, X, Y は整数
- 1 \leq N \leq 14
- 1 \leq X,Y \leq 10^8
- C_i は
XまたはY - A_i, B_i は整数
- -10^8 \leq A_i, B_i \leq 10^8
入力
入力は以下の形式で標準入力から与えられる。
N X Y C_1 A_1 B_1 \vdots C_N A_N B_N
出力
2 行出力せよ。
1 行目には、黒いマスからなる連結成分の個数を出力せよ。
2 行目には、各連結成分におけるマスの個数を、空白区切りで昇順に出力せよ。
入力例 1
2 3 5 X 2 2 Y -1 1
出力例 1
2 2 13
大嵐によって、グリッドは以下の画像のように変化します(右方向が x 軸の正の向き、上方向が y 軸の正の向き)。
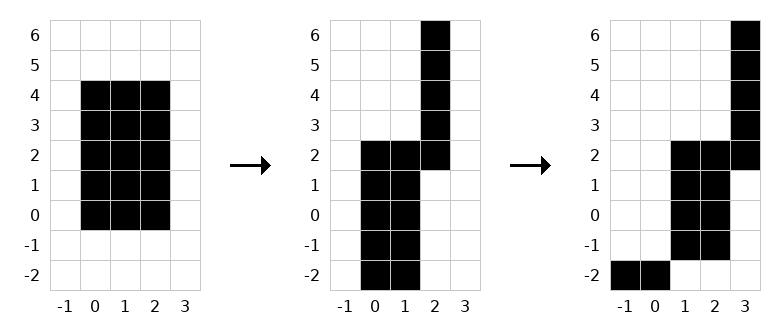
最終的なグリッドにおいて、以下の 2 つの連結成分が存在します。
- マス (-1,-2), (0,-2) からなる連結成分。
- マス (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6) からなる連結成分。
各連結成分がもつマスの個数は昇順に出力する必要があることに注意してください。
入力例 2
14 68875272 94216928 X 1630731 32914676 X 17164413 -33684569 X 26798060 5418308 X 34094469 -45675954 X 43889566 34125482 X 56836569 -22217058 X 64045210 27857939 Y -54561094 11587606 Y 93548188 32214521 Y -77361096 25750481 Y 27724899 1810420 Y 80945185 -7871305 Y 14782822 -2565089 Y 54687684 -22884393
出力例 2
8 21105046168287 22050167303226 33624667752182 223328231190194 441936776830492 1141371400772596 1141702254882183 3464097998105256
出力する値は 32bit 整数に収まらないことがあります。
Score : 425 points
Problem Statement
There is an infinitely large two-dimensional grid. The color of cell (x,y) is black if 0 \leq x \leq X-1 and 0 \leq y \leq Y-1, and white otherwise.
N great storms occur in order on this grid. The i-th great storm updates the color of each cell on the grid according to a rule represented by a character C_i and integers A_i, B_i.
In the i-th great storm, the color of cell (x, y) after the great storm is:
- In case C_i is
X,- if x < A_i, it becomes the color of cell (x, y + B_i) before the great storm;
- if x \geq A_i, it becomes the color of cell (x, y - B_i) before the great storm.
- In case C_i is
Y,- if y < A_i, it becomes the color of cell (x + B_i, y) before the great storm;
- if y \geq A_i, it becomes the color of cell (x - B_i, y) before the great storm.
Two black cells (x_1, y_1), (x_2, y_2) are adjacent if and only if |x_1 - x_2| + |y_1 - y_2| = 1. Also, two black cells c_1, c_2 are connected if and only if one can move from cell c_1 to cell c_2 by repeatedly moving to adjacent black cells.
A non-empty set S of black cells is a connected component if and only if S satisfies the following conditions:
- Any two cells in S are connected.
- Every black cell not in S is not connected to any cell in S.
For the grid after all N great storms have occurred, find the number of connected components and output the number of cells in each connected component in ascending order.
Constraints
- N, X, Y are integers.
- 1 \leq N \leq 14
- 1 \leq X,Y \leq 10^8
- C_i is
XorY. - A_i, B_i are integers.
- -10^8 \leq A_i, B_i \leq 10^8
Input
The input is given from Standard Input in the following format:
N X Y C_1 A_1 B_1 \vdots C_N A_N B_N
Output
Output two lines.
The first line should contain the number of connected components consisting of black cells.
The second line should contain the number of cells in each connected component, space-separated, in ascending order.
Sample Input 1
2 3 5 X 2 2 Y -1 1
Sample Output 1
2 2 13
The grid changes as shown in the following image due to the great storms (the rightward direction is the positive direction of the x-axis, and the upward direction is the positive direction of the y-axis).

In the final grid, the following two connected components exist:
- A connected component consisting of cells (-1,-2), (0,-2).
- A connected component consisting of cells (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6).
Note that the number of cells in each connected component must be output in ascending order.
Sample Input 2
14 68875272 94216928 X 1630731 32914676 X 17164413 -33684569 X 26798060 5418308 X 34094469 -45675954 X 43889566 34125482 X 56836569 -22217058 X 64045210 27857939 Y -54561094 11587606 Y 93548188 32214521 Y -77361096 25750481 Y 27724899 1810420 Y 80945185 -7871305 Y 14782822 -2565089 Y 54687684 -22884393
Sample Output 2
8 21105046168287 22050167303226 33624667752182 223328231190194 441936776830492 1141371400772596 1141702254882183 3464097998105256
The output value may not fit in a 32-bit integer.