D - RLE Moving 解説 by en_translator
This problem can be solved with a carefully designed simulation.
First, consider the following problem:
Problem (★) Takahashi starts from \((R_t,C_t)\) and moves in direction \(D_t\), and Aoki starts from \((R_a,C_a)\) and moves in direction \(D_a\). They move by one square in one move. Determine if they will visit the same square at the same time, and find the minimum number of moves when such an event occurs if it will happen.
This problem can be solved in \(O(1)\) time, but be careful of the case \(D_t=D_a\).
Now consider the original problem. While Aoki and Takahashi are moving in their respective constant directions, the sought answer can be computed according to Problem (★) at once. Therefore, the original problem can be answered by solving Problem (★) \(O(M+L)\) times, and the time complexity is \(O(M+L)\).
For example, if Takahashi’s move is LLLUURRRR and Aoki’s is DUUUUUULL, we can split into the following five segments:
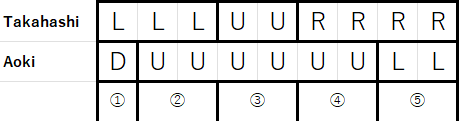
投稿日時:
最終更新: