 /
/ 
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 475 点
問題文
二次元平面上に N 個の点があり、i 番目の点は座標 (X_i, Y_i) にあります。どの 2 点も相異なる位置にあり、どの 3 点も同一直線上にないことが保証されます。
これらの点から 4 点を選ぶ組合せのうち、その 4 点を頂点とする多角形として台形がとれるものは何通りありますか?
制約
- 4 \leq N \leq 2\,000
- 0 \leq X_i, Y_i \leq 10^7 (1 \leq i \leq N)
- どの 2 点も相異なる位置にある。
- どの 3 点も同一直線上にない。
- 入力される値は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N X_1 Y_1 \vdots X_N Y_N
出力
答えを 1 行に出力せよ。
入力例 1
5 0 2 0 5 1 0 2 1 2 4
出力例 1
3
与えられた点は、以下の図のような配置になっています。
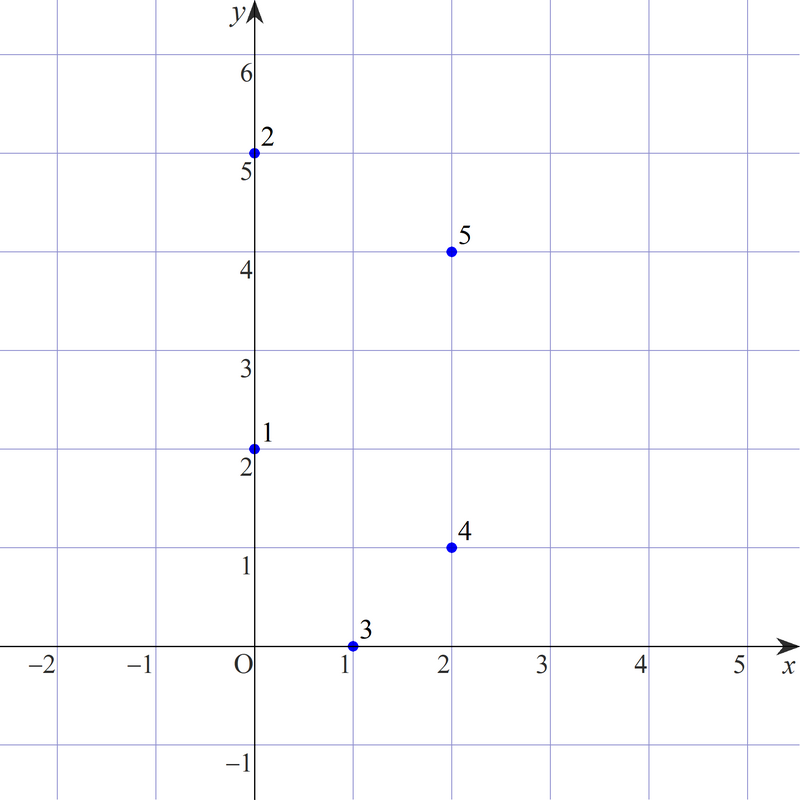
ここから 4 点を選ぶ組合せのうち、それらを頂点とする台形がとれるものは以下の 3 通りです。
- 1,5,4,3 番目の点。
- 1,3,4,2 番目の点。
- 1,2,5,4 番目の点。
平行四辺形や長方形も台形の一種として扱うことに注意してください。
入力例 2
8 0 1 1 3 2 3 3 1 0 2 1 0 2 0 3 2
出力例 2
22
Score : 475 points
Problem Statement
There are N points on a two-dimensional plane, with the i-th point at coordinates (X_i, Y_i). It is guaranteed that no two points are at the same position, and no three points are collinear.
Among the combinations of four points from these points, how many combinations can form a trapezoid as a polygon with those four points as vertices?
Constraints
- 4 \leq N \leq 2\,000
- 0 \leq X_i, Y_i \leq 10^7 (1 \leq i \leq N)
- No two points are at the same location.
- No three points are collinear.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X_1 Y_1 \vdots X_N Y_N
Output
Print the answer on one line.
Sample Input 1
5 0 2 0 5 1 0 2 1 2 4
Sample Output 1
3
The given points are arranged as shown in the figure below.

Among the combinations of four points, the following three combinations can form a trapezoid as a polygon with those points as vertices:
- The 1st, 5th, 4th, 3rd points.
- The 1st, 3rd, 4th, 2nd points.
- The 1st, 2nd, 5th, 4th points.
Note that parallelograms and rectangles are also treated as trapezoids.
Sample Input 2
8 0 1 1 3 2 3 3 1 0 2 1 0 2 0 3 2
Sample Output 2
22