Preface

This problem has several possible approaches.
One of the most naive one is to solve the problem for the 16 possible combinations of \((A,B,C,D)\) separately. While this does not require an advanced knowledge, it is problematic because it is trouble and takes long time. (The author estimates that even crown-coders who are good at solving fast would need no less than 40 minutes.) Solve this problem within the contest time would require a high information processing capability.
In this editorial, we introduce a way to solve the problem using the properties of automata and regular languages.

Outline of Solution

As usual, this article is going to be lengthy, so we will present you the outline first.
This problem is closely related to automata. As an instance, let us consider \((A,B,C,D)=(1,0,0,1)\), which is equivalent to Problem D.
In Problem D, a string is beautiful if and only if it contains an even number of 0s. To that end, we can construct an automaton containing the following three states:

• A state that accepts an empty string (\(\varepsilon\) in the figure below)
• A state that accepts an non-empty string containing an odd number of 0s (\(\mathrm{o}\) in the figure below)
• A state that accepts an non-empty string containing an even number of 0s (\(\mathrm{e}\) in the figure below)

This automaton is designed to recognize beautiful strings at state \(\mathrm{e}\).

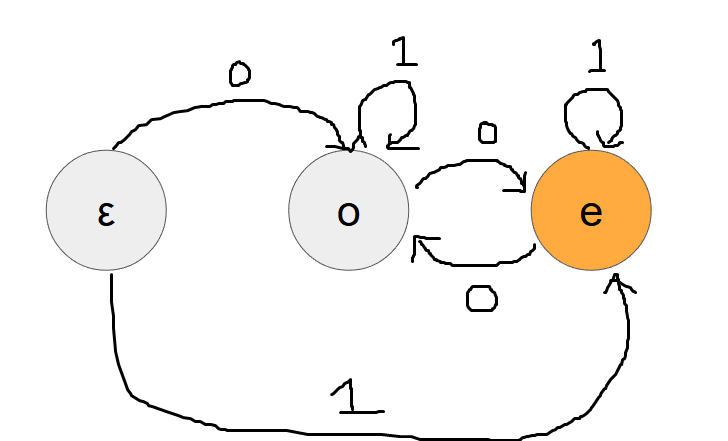
The problem can be solved by performing a DP (Dynamic Programming) according to the form of this automaton.

With this fact in mind, we claim the following proposition:

• For any \((A,B,C,D)\), there is an automaton that recognizes beautiful strings.

For now, let us accept this proposition. By the way, when there exists an automaton that recognizes beautiful strings, this time we can construct an algorithm that guesses the form of the automaton out of nowhere (!). Since this algorithm allows us to obtain automata for all \((A,B,C,D)\), the proposition above turns out to be true. Moreover, since we can assert that each automaton contains at most \(7\) vertices, all that left is to perform DP according to the automaton obtained, to solve the problem in \(O(N)\) time. This is the outline of this problem.

Before diving into the solution, let us overview the concept of automaton, and a deeply related idea regular language.

Automaton

Let us define notations first:

• \(\Sigma\) represents the alphabet (the set of letters). \(\Sigma^{\ast}\) denotes the strings, which are sequences of letters in the alphabet.
• \(\varepsilon\) represents an empty string.
• The concatenation of strings \(x\) and \(y\) in order is denoted by \(xy\).
• A power of string \(x\) is the concatenation of \(n\) copies of \(x\), denoted by \(x^n\).

We also define a language (a set of strings) likewise.

• For languages \(X\) and \(Y\), define \(XY := \lbrace xy \vert x \in X, y \in Y \rbrace\).
• For a language \(X\) and a positive integer \(n\), define \(X^n := \lbrace x_1 x_2 \dots x_n \vert x_1, x_2, \dots, x_n \in X \rbrace\).
• For a language \(X\), define \(X^\ast := \bigcup_{n\geq 0} X^n = \lbrace \varepsilon \rbrace \cup X^1 \cup X^2 \cup \dots \) (called Kleene closure).

An automaton (plural form: automata) is a state machine that determines if a given string is contained in a string. (Detailed explanation is omitted.) In this article, we only handle finite automata, which contain a finite number of states.
A finite automaton is classified into two types: Deterministic (Finite) Automaton (DFA) and Non-deterministic (Finite) Automaton (NFA).
A DFA is an automaton where the current state and the next character uniquely determines the next state. For example, the automaton introduced above is a DFA.
An NFA is an automaton where the current state and the next character do not necessarily uniquely determine the next state. In other words, the final state for a given string is not necessarily unique.
Any NFA can be transformed into an equivalent DFA. (This is called a powerset construction; simply put, it can be constructed in the same manner as bit DP.)

Regular Language

Let \(L(M)\) denote the language that is recognized by an automaton \(M\). Such a language is, in fact, called a regular language.

The set of regular languages is defined recursively as follows:

• An empty language \(\emptyset\) is a regular language.
• For any letter \(a \in \Sigma\) in the alphabet, the language \(\lbrace a \rbrace\) containing only the single-letter string \(a\) is a regular language.
• When \(X\) and \(Y\) are regular languages, \(X \cup Y\) is also a regular language.
• When \(X\) and \(Y\) are regular languages, \(X Y\) is also a regular language.
• When \(X\) is a regular language, \(X^{\ast}\) is also a regular language.

Here, we can prove that the following two propositions are equivalent:

1. A language \(L\) is recognized by a finite automaton \(M\).
2. A language \(L\) is a regular language.

We omit the proof here, but roughly speaking, we can assert that an NFA can be transformed based on each operation on regular languages.

Minimizing the number of states in a DFA

An observation implies that there exists a pair of distinct DFAs \(M_1\) and \(M_2\) such that the generated languages \(L(M_1)\) and \(L(M_2)\) are equal. Conversely, we can also assert that there exist an infinite number of DFAs that recognize the same language \(L\).
If there are multiple DFAs that recognize a language \(L\), then we naturally want to think about a DFA with the minimum number of states. So let us start thinking about this state number minimization problem.

First, given a DFA \(M\), one can find an equivalent DFA with the minimum number of states with the following simple algorithm: identify all accepted and non-accepted states in a single set, then divide the set every time you find a set containing elements pointing toward different states. The algorithm can be implemented to run in \(\mathrm{O}(n^2 \vert \Sigma \vert)\) time, if \(M\) has \(n\) states. (We omit the details here; think about it.)

Now, given a language \(L\), what are the properties satisfied by DFAs recognizing \(L\) with the minimum number of states? The following Myhill-Nerode theorem characterizes such DFAs:

Myhill-Nerode theorem

For a language \(L\) and strings \(x\) and \(y\), define a relation \(\sim_L\) as: \(xz \in L \iff yz \in L\) for all strings \(z\).
Then \(\sim_L\) is an equivalence relation, and the following propositions are equivalent:

1. The language \(L\) is a regular language.
2. The number of the equivalence classes of \(\sim_L\) is finite.

Moreover, the DFA with the minimum number of states has the same number of states as the number of the equivalence classes.

Here, recall the definitions of equivalence relation and equivalence class:

For a set \(S\), a binomial relation that satisfies the following properties is called an *equivalence relation:

• Reflexibility: \(\forall a \in S, a \sim a\)
• Symmetry: \(\forall a, b \in S, a \sim b \to b \sim a\)
• Transitivity: \(\forall a,b,c \in S, (a \sim b \wedge b \sim c) \to a \sim c\)

Given a set \(S\), an equivalence relation \(\sim\), and an element \(a\) in \(S\), we call \(\lbrace x \in S \mid x \sim a \rbrace\) the equivalence class of \(a\). The set of the equivalence classes comprise a partition of the set \(S\).

Intuitively, the theorem claims that:

• Any prefix of a string in a regular language can be classified by the “semantics” into a finite number of groups, and
• Assigning a state to each of the groups of “semantics” form a DFA with the minimum number of states.

(Outline of Proof) We omit the proof that \(\sim_L\) is an equivalence class. We will show that 1. and 2. are equivalent.
1 -> 2: If \(L\) is a regular language, then there exists a DFA \(M\) that recognizes \(L\). Suppose that there are an infinite number of equivalence classes. Take ((# states in \(M\)) \(+1\)) classes and pick an element from each of them. Then by Pigeonhole Principle, there exist strings \(x\) and \(y\) that falls to the same state in the DFA. However \(x \sim_L y\) holds, which is a contradiction. Thus, the number of equivalence classes is finite. 2 -> 1: Given a set of equivalence classes, one can construct a DFA that recognizes \(L\) as follows, so \(L\) turns out to be a regular language:

• Define a state for each equivalence class.
• Let the initial state to be the equivalence class of \(\varepsilon\).
• When you are at an equivalence class represented by \(x\) and encounter a character \(c\), advance to the one represented by \(xc\).
• The acceptance states are the equivalence classes containing the strings accepted by \(L\).

Here, one can prove that the DFA constructed in the proof for 2->1 has the minimum number of states. Roughly, it can be proved as follows: if the number of states is more than the number of equivalence classes, then we can take one element from each state to find a pair with \(x \sim_L y\) by Pigeonhole Principle, which in turn allow us to merge the states for \(x\) and \(y\) to reduce states. This concludes the outline of the solution.

So far, we have gone through the knowledge of automata and regular languages, which are required for the explanation of the problem. Next, we will describe the solution.

Solution to the Problem

For each \((A,B,C,D)\), we assume that the set of beautiful strings \(L\) is a regular language and aim at constructing an automaton.
Recall the equivalence relation \(\sim_L\) in Myhill-Nerode theorem: \(xz \in L \iff yz \in L\) for all strings \(z\).
We want to know the equivalence class of \(\sim_L\), but checking \(xz \in L \iff yz \in L\) for all \(z\) is impossible. Instead, consider obtaining a DFA \(M\) by the following algorithm:

• For \(u=0, 1, 2, \dots\) in order:
  • Define an equivalence relation \(\sim_{L,u}\) as: \(xz \in L \iff yz \in L\) for all strings \(z\) of length less than or equal to \(u\).
  • Let \(M_u\) be the DFA based on the equivalence classes of \(\sim_{L,u}\).
  • If \(u \gt 0\), and \(M_u\) and \(M_{u-1}\) are equivalent, report \(M = M_u\) and terminate the algorithm.

Here, \(M_u\) is the DFA obtained by the BFS (Breadth-First Search) represented by the following Python-like psuedocode. (\(M_u\) looks similar to a Trie. Although not explained in the pseudocode, the initial state of \(M_u\) is the state whose representative element is ε.)

Z = (The set of strings of lengths u or less, including ε)

def get(x):

  xz_list = list()
  for z in Z:
    xz = x + z
    xz_list.append(1 if xz in L else 0)
  return xz_list

memo = dict()
Q = queue()
Q.add(ε)
while Q is not empty:
  x = Q.pop()
  if not get(x) in memo:
    memo[get(x)] = x
    Q.add(x + '0')
    Q.add(x + '1')

M_u = list()
for x, _ in memo:
  # The representative element of the state
  leader = x
  # If you find '0', transition to:
  x0 = memo[get(x + '0')]
  # If you find '1', transition to:
  x1 = memo[get(x + '1')]
  # Is it an accepted state?
  accept = 1 if x in L else 0
  M_u.append((leader, x0, x1, accept))

One can prove that \(M\) obtained by the algorithm above is a DFA that recognizes \(L\). (Note that this algorithm is valid only in this problem.)

(Proof) Let \(L_u\) be the language recognized by \(M_u\). Let \(V_u\) be a set of representative elements of the states in \(M_u\). One can check that \(M_u\) and \(L_u\) has the following property:

• Let \(W_u = V_u \cup \lbrace x0 \mid x \in V_u \rbrace \cup \lbrace x1 \mid x \in V_u \rbrace\). (\(x0\) denotes the string obtained by appending \(0\) to \(x\); same for \(x1\).)

By the same discussion as Myhill-Nerode theorem, one can prove that \(M_u\) is the DFA with the minimum number of states of the language that allows us to minimize the state count among the languages satisfying the property above; in fact, such a DFA and a language is unique. (Proof omitted.) Next, consider the \(u\) where \(M_u = M_{u+1}\) is satisfied for the first time. By the property of the operation, one can construct based on \(M_u\) a NFA \(M'_{u+1}\) that accepts \(xz\) for all \(x \in W_u\) and all strings \(z\) of length \(u+1\) or less. Furthermore, transform it into a DFA and minimize the number of states, denoted by \(M''_{u+1}\). This procedure transforms \(M_u\) into \(M''_{u+1}\), but by the uniqueness of the DFA with the minimum number of states proved above, it turns out that \(M''_{u+1} = M_{u+1}\). This implies that one can transform \(M_u\) into \(M_{u+1}\) via a NFA. Repeatedly applying it shows that \(M_u = M_{u+1} = M_{u+2} = \dots\), implying that \(M_u\) is a DFA that recognizes \(L\). (End of proof)

By actually running the algorithm for all \((A,B,C,D)\), one can assert that the algorithm terminates within \(u \leq 3\), and any obtained DFA \(M\) has \(7\) or less states. Therefore, the algorithm above yields a DFA fast enough, and the obtained \(M\) allows us to solve the problem in \(\mathrm{O}(N)\) time, which is fast enough.

References

We referred to the following articles to write the problem and the editorial.

• XX Open Cup Grand Prix of Tokyo, Problem J: Median Replace Hard
• 浅谈有限状态自动机及其应用(徐哲安, 2021 年信息学奥林匹克中国国家集训队论文集)