Editorial - AtCoder Beginner Contest 418

Contest Duration: 2025-08-09 21:00:00+0900 - 2025-08-09 22:40:00+0900 (local time) (100 minutes) Back to Home

Official

G - Binary Operation Editorial by Nyaan

はじめに

この問題はいくつかの方針が考えられる問題です。
素直な方針として、 \((A,B,C,D)\) の 16 通りの組み合わせ全てに対して別々に問題を解くという方法があります。これは難しい考察を要求しない方針ですが、極めて面倒で時間が掛かるという問題があります。(早解きが得意なタイプの冠コーダーでも 40 分はかかると筆者は予想しています。) この方針で今回の問題を時間内に解き切るには高い情報処理能力が必要でしょう。
この解説では オートマトン および 正規言語 の持つ性質を利用して解く方法を解説します。

解法の概要

この解説は例のごとく長くなりそうなので、簡単な概要を先に示します。
今回の問題とオートマトンは密接な関係にあります。例として、D 問題、すなわち \((A,B,C,D)=(1,0,0,1)\) のケースをオートマトンを用いて解く方法を説明します。
D 問題においては、美しい文字列の必要十分条件は「0 を偶数個含む非空な文字列」です。この時、

空文字列を意味する状態(図の \(\varepsilon\))
0 を奇数個含む非空な文字列を意味する状態(図の \(\mathrm{o}\))
0 を偶数個含む非空な文字列を意味する状態(図の \(\mathrm{e}\))

の \(3\) 状態からなる美しい文字列を受理するオートマトンを構成すると下図になります。(\(\mathrm{e}\) が受理状態です)

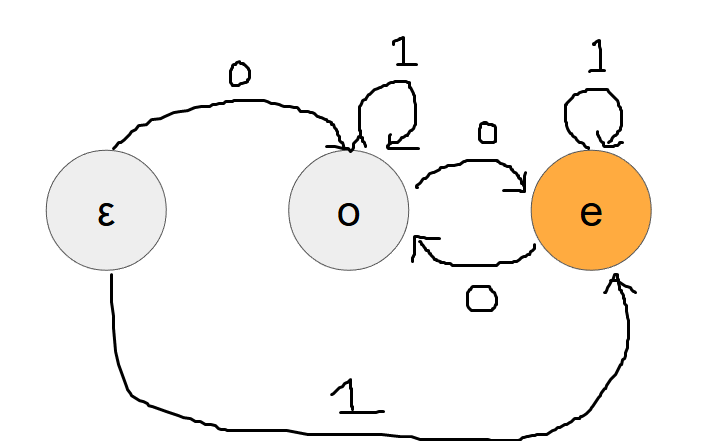
このオートマトンの形状に従って動的計画法(DP) を行うと問題を解くことが出来ます。

このような事実を踏まえたうえで、次の命題を置きます。

任意の \((A,B,C,D)\) において、美しい文字列を受理するオートマトンが存在する。

この命題をいったん正しいと信じることにします。ところで実は、美しい文字列を受理するオートマトンが存在する時に、そのオートマトンの形をエスパーするアルゴリズムを今回は構成できます(!)。そのアルゴリズムを使用すると、任意の \((A,B,C,D)\) についてオートマトンを求めることが出来るので、上記の命題は正しいことがわかります。また、オートマトンの頂点数は高々 \(7\) 頂点であることも確認できるので、あとはオートマトンの形に従って DP すれば各問題を \(\mathrm{O}(N)\) で解くことができます。これが今回の問題の解法の概要です。

解法の詳細を説明するために、次章からは オートマトン、およびそれと深い関わりを持つ 正規言語 について簡単に概観します。

オートマトン

はじめに文字列の表記に関していくつかの定義を行います。

アルファベット (いわゆる文字) の集合を \(\Sigma\) として表す。アルファベットを並べたものを 文字列 と定義して \(\Sigma^{\ast}\) と表す。
空文字列を \(\varepsilon\) と表す。
文字列 \(x\) と文字列 \(y\) をこの順に並べて結合して得られる文字列を連接と呼び \(xy\) と表す。
文字列 \(x\) を \(n\) 個結合して得られる文字列を累乗と呼び \(x^n\) と表す。

言語 (文字列の集合) についても同様の定義を行います。

言語 \(X, Y\) について \(XY := \lbrace xy \vert x \in X, y \in Y \rbrace\) とする。
言語 \(X\) および正整数 \(n\) について \(X^n := \lbrace x_1 x_2 \dots x_n \vert x_1, x_2, \dots, x_n \in X \rbrace\) とする。
言語 \(X\) について \(X^\ast := \bigcup_{n\geq 0} X^n = \lbrace \varepsilon \rbrace \cup X^1 \cup X^2 \cup \dots \) とする。(これを クリーネ閉包 と呼ぶ。)

オートマトン とは、いくつかの状態と遷移規則に基づいて、ある文字列が言語に含まれるかどうかを判定する機械です。(詳細な説明は割愛します) ここでは状態数が有限個である 有限オートマトン のみを取り上げます。
有限オートマトンは 決定性オートマトン (DFA) と 非決定性オートマトン(NFA) の 2 種類に分かれます。
DFA とは、現在と次の文字が決まれば次の状態が 1 通りに定まるオートマトンです。例えば先に挙げたオートマトンは DFA です。
NFA とは、現在と次の文字が決まった時の遷移先が 1 通りとは限らないオートマトンです。すなわち、文字列が与えられたときに最終状態として複数の状態を取り得るオートマトンであると言えます。
全ての NFA は等価な DFA に変換できます。(これは powerset construction と呼ばれていて、簡単に言うと bit DP の要領で構成できます。)

正規言語

有限オートマトン \(M\) が受理する言語を \(L(M)\) とします。実はそのような言語には 正規言語 という名前がついています。

正規言語の集合は以下の手順により再帰的に定義されます。

空の言語 \(\emptyset\) は正規言語である。
任意のアルファベット \(a \in \Sigma\) について、\(a\) 1 文字からなる文字列のみを含む言語 \(\lbrace a \rbrace\) は正規言語である。
\(X\) と \(Y\) が正規言語であるとき、\(X \cup Y\) は正規言語である。
\(X\) と \(Y\) が正規言語であるとき、\(X Y\) は正規言語である。
\(X\) が正規言語であるとき、\(X^{\ast}\) は正規言語である。

ここで、次の 2 つの命題が等価であることが証明できます。

言語 \(L\) を有限オートマトン \(M\) が受理する。
言語 \(L\) が正規言語である。

証明は省略しますが概要としては、正規言語の各演算に対応した NFA の変形が可能であることから正規言語を NFA に変換できる、という手順となっています。

DFA の状態数最小化

観察により、異なる DFA の組 \(M_1, M_2\) であってそれらが生成する言語 \(L(M_1), L(M_2)\) が等しいものが存在することに気づきます。また、逆に正規言語 \(L\) を決め打った時にそれを受理する DFA は無数に存在することが言えます。
言語 \(L\) を受理する DFA が複数あるのであれば、そのうち状態数が最小であるものが最も扱いやすそうです。というわけで DFA の状態数を最小化する問題について考えてみましょう。

まず、 DFA \(M\) が与えられた時に \(M\) と等価な DFA であって状態数が最小であるものを発見する問題は、「はじめは全ての受理状態・非受理状態をそれぞれ同一視して 1 つの集合に入れて、そこから遷移先が異なる要素たちが含まれた集合を発見するたびに集合を分割する」というシンプルなアルゴリズムで \(M\) の状態数を \(n\) として \(\mathrm{O}(n^2 \vert \Sigma \vert)\) 程度で計算できます。(詳細は省略します。考えてみましょう)

では、正規言語 \(L\) に対して、それを受理する状態数最小の DFA はどのような性質を持つのでしょうか？この問いに対して、次に説明する Myhill-Nerode の定理 が状態数最小の DFA の特徴付けを与えます。

Myhill-Nerode の定理

言語 \(L\) および文字列 \(x, y\) に対して関係 \(\sim_L\) を次のように定める：任意の文字列 \(z\) に対して \(xz \in L \iff yz \in L\) が成り立つ。
この時、\(\sim_L\) は同値関係となる。そして、次の 2 つの命題は同値である。

言語 \(L\) は正規言語である。

文字列全体に対する \(\sim_L\) の同値類の個数は有限である。

そして、状態数最小の DFA の状態数は同値類の個数と一致する。

ここで、同値関係および同値類の定義を確認します。

ある集合 \(S\) において以下を全て満たす二項関係 \(\sim\) を \(S\) 上の 同値関係 と呼ぶ。

反射律 \(\forall a \in S, a \sim a\)

対称律 \(\forall a, b \in S, a \sim b \to b \sim a\)

推移律 \(\forall a,b,c \in S, (a \sim b \wedge b \sim c) \to a \sim c\)

集合 \(S\)、同値関係 \(\sim\)、\(S\) の元 \(a\) に対して、\(\lbrace x \in S \mid x \sim a \rbrace\) を \(a\) の 同値類 と呼ぶ。同値関係の定義から、同値類たちの集合は \(S\) の分割になる。

定理を直感的に説明すると、

正規言語に含まれる文字列の先頭部分を “意味” の違いで分類しても有限個にしかならず、
その “意味” が違う分類たちに 1 個の状態を割り当てるとそれが状態数最小の DFA になる

ということになります。

(証明の概要) \(\sim_L\) が同値関係である証明は割愛します。1. と 2. が同値であることを示します。
1 -> 2: 言語 \(L\) が正規言語であれば、\(L\) を受理する DFA \(M\) が存在します。同値類が無限に存在すると仮定します。同値類を (\(M\) の状態数) \(+1\) 個選んでそれぞれの同値類から元を 1 つ取り出すと、鳩ノ巣原理よりその中に DFA 上で同じ状態を取る文字列 \(x, y\) が存在します。しかしこのとき \(x \sim_L y\) が成り立つので矛盾が発生します。以上より同値類の個数は有限です。
2 -> 1: 同値類を元に以下の手順で言語 \(L\) を受理する DFA を構成できるので、\(L\) は正規言語であることがいえました。

各同値類を 1 つの状態とする。
初期状態は \(\varepsilon\) の同値類とする。
\(x\) を元に持つ同値類に文字 \(c\) を追加した時は \(xc\) を元に持つ同値類に遷移する。
\(L\) で受理される文字列を含む同値類を受理状態とする。

ここで、2->1 の証明において構築した DFA が実際に状態数最小を達成する DFA であることが証明できます。簡単に説明すると、状態数が同値類の個数よりも多い DFA であれば各状態から元を 1 個ずつ取ってくると鳩ノ巣原理より \(x \sim_L y\) である組を発見できて、\(x\) に対応する状態と \(y\) に対応する状態をマージして問題ないため状態数を減らせる、という方針で証明できます。以上が証明の概要となります。

問題の解説に必要なオートマトンと正規言語の知識を概観しました。次は問題の解説に移ります。

問題の解法

各 \((A,B,C,D)\) に対して、美しい文字列からなる集合 \(L\) が正規言語であることを仮定してオートマトンを構成することを目標とします。
文字列を Myhill-Nerode の定理の同値関係 \(\sim_L\) を再掲します : 任意の文字列 \(z\) に対して \(xz \in L \iff yz \in L\) が成り立つ。
\(\sim_L\) の同値類を計算できればよいですが、全ての \(z\) に対して \(xz \in L \iff yz \in L\) を判定することは不可能です。そこで、次のアルゴリズムによって DFA \(M\) を得ることを考えます。

\(u=0, 1, 2, \dots\) の順に次の操作を行う。
- 同値関係 \(\sim_{L,u}\) を「任意の長さ \(u\) 以下の文字列 \(z\) に対して \(xz \in L \iff yz \in L\) が成り立つ」と定義する。
- \(\sim_{L,u}\) 上の同値関係に基づく DFA を \(M_u\) とする。(DFA を手に入れる方法は後述)
- \(u \gt 0\) かつ \(M_u\) と \(M_{u-1}\) が等価である場合、\(M = M_u\) としてアルゴリズムを終了する。

ここで \(M_u\) は次の Python 風の疑似コードで表される BFS によって得る DFA とします。(\(M_u\) は Trie 木に似た形になります。疑似コードに載っていませんが \(M_u\) の初期状態は代表元が ε である状態です。)

Z = (長さ u 以下の文字列からなる集合, ε を含む)

def get(x):
  xz_list = list()
  for z in Z:
    xz = x + z
    xz_list.append(1 if xz in L else 0)
  return xz_list

memo = dict()
Q = queue()
Q.add(ε)
while Q is not empty:
  x = Q.pop()
  if not get(x) in memo:
    memo[get(x)] = x
    Q.add(x + '0')
    Q.add(x + '1')

M_u = list()
for x, _ in memo:
  # 状態の代表元
  leader = x
  # '0' に対応する遷移先
  x0 = memo[get(x + '0')]
  # '1' に対応する遷移先
  x1 = memo[get(x + '1')]
  # 受理状態かどうか
  accept = 1 if x in L else 0
  M_u.append((leader, x0, x1, accept))

さて、前述のアルゴリズムによって得られる \(M\) は \(L\) を受理する DFA であることが証明できます。(このアルゴリズムは今回の問題でのみ成り立つアルゴリズムである点に注意してください。)

(証明) \(M_u\) が受理する言語を \(L_u\) とします。また、 \(M_u\) の各状態の代表元からなる集合を \(V_u\) とします。\(M_u\) および \(L_u\) は次の性質を持つことが確認できます。

\(W_u = V_u \cup \lbrace x0 \mid x \in V_u \rbrace \cup \lbrace x1 \mid x \in V_u \rbrace\) とする。(ここで \(x0\) は \(x\) の末尾に \(0\) を加えた文字列。\(x1\) も同様)
\(x \in W_u\) を満たす \(x\) および長さ \(u\) 以下の文字列 \(z\) について \(xz \in L \iff xz \in L_u\) が成り立つ。

また、Myhill-Nerode の定理と同様の議論を行うことで、\(M_u\) が上記の性質を持つ言語のうち DFA の状態数を最小化できる言語を選んで最小化した DFA であり、またそのような言語および DFA は一意に定まることが証明できます。(詳細は略します)
次に、\(M_u = M_{u+1}\) が初めて成り立つ \(u\) について考えます。操作の性質により、\(M_u\) を利用して、任意の \(x \in W_u\) および任意の長さ \(u+1\) 以下の文字列 \(z\) に対して \(xz\) を受理する NFA \(M'_{u+1}\) を構築できます。そして \(M'_{u+1}\) を DFA に変換して状態数を最小化したものを \(M''_{u+1}\) と置きます。このような手順によって \(M_u\) から \(M''_{u+1}\) を得られますが、上記の状態数最小の DFA の一意性から \(M''_{u+1} = M_{u+1}\) であることが示せます。よって \(M_u\) から NFA を経由した変換によって \(M_{u+1}\) を得られることが言えました。この操作を繰り返すことで \(M_u = M_{u+1} = M_{u+2} = \dots\) が成り立ち、\(M_u\) が \(L\) を受理する DFA であることが従います。(証明終わり)

実際に全ての \((A,B,C,D)\) において実験すると、\(u \leq 3\) の範囲でアルゴリズムが終了して、かつ得られる DFA \(M\) の状態数は \(7\) 以下となることが確認できます。よって上記のアルゴリズムで DFA を十分高速に得られて、 \(M\) を元に答えを計算すればこの問題を \(\mathrm{O}(N)\) で解くことが出来て、これは十分高速です。

参考資料

今回の出題および解説執筆は以下を参考にしました。

posted:
last update: