Suppose that when we remove chords at the beginning of the procedure, we remove not only those that intersect with others, but also those which do not contribute to the final answer.

That means we leave chords in the following form:

More precisely

The chords to be left, denoted by chords $1,\ldots,k$, satisfy the following: there exists a permutation $(i_1,\ldots,i_k)$ of $(1,\ldots,k)$ and a point $P$ on the circle such that, if we traverse the circle from $P$ clockwise, we encounter an endpoint of chord $i_1$, endpoint of $i_2$, $\ldots$, endpoint of $i_k$, the other endpoint of $i_k$, of $i_{k-1}$, $\ldots$, and of $i_1$, in this order.

Proof

Let $P$ and $Q$ be the endpoints of the chord added lastly. The condition is satisfied by letting the chords crossed when traveling from $P$ to $Q$ be $i_1,\dots,i_k$ in order. (Since the chords $1,\ldots,k$ do not intersect with each other, the encountering order along arc $PQ$ is the same as the crossing order along line segment $PQ$.)

Conversely, if the chords are left in the form above, then one can add a chord that intersect with all of them.

Proof

One can take an arbitrary point $Q$ on the arc formed by the chord $i_k$ not containing point $P$, and add a chord connecting $P$ and $Q$.

Let us open the circle into a line, in order to consider intervals instead of chords.

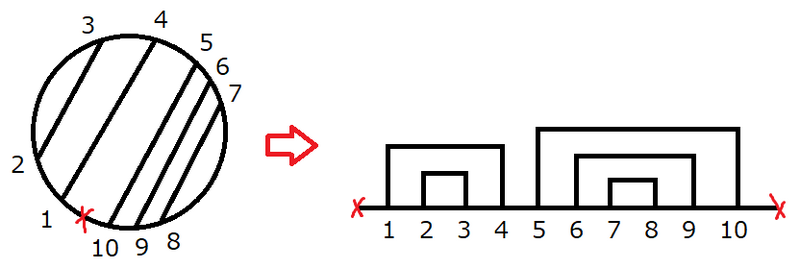
By this transformation, the original problem is reduced into the following:

You are given \(N\) intervals on a number line. How many intervals \(I_1,\ldots,I_k\) at maximum can you choose so that one of the following is satisfied?

• \(I_1 \subset\dots\subset I_{k}\)
• There exists \(1\leq k' < k\) such that \(I_1 \subset\dots\subset I_{k'}\) and \(I_{k'+1}\subset\dots\subset I_k\) and \(I_{k'}\cap I_k=\emptyset\).

Proof

Proof that a solution to the rephrased problem is a solution to the original problem: For the former case, we can take $P$ inside $I_1$ and $Q$ outside $I_k$. For the latter case, we can take $P$ inside $I_1$ and $Q$ inside $I_{k'+1}$.
Proof that a solution to the original problem is a solution to the rephrased problem: identify a chord in the original problem with the corresponding interval after the transformation. Let $R$ be the point on the circle that was cut when opening the circle. Call the chords within the arc $PR$ not containing $Q$ chords $1,2,\ldots,k'$, numbered from $P$ in order; call those withing arc $RQ$ not containing $P$ chords $k'+1,\ldots,k$, numbered from $Q$ in order.

If there are intervals \(I_1 \subset I_2 \subset\dots\subset I_k\), let us say they are nested.

We assume that the given intervals \(I_i=[L_i,R_i]\) are sorted in ascending order of \(R_i\).

Former case

The answer is the length of a longest monotonically-decreasing subsequence of \(L_i\), which can be found using a segment tree in \(O(N\log N)\) time.

Proof

Because $I_i \subset I_2 \subset \ldots \subset I_k \iff L_k\leq L_{k-1}\leq \ldots \leq L_1 \leq R_1 \leq R_2 \leq \ldots \leq R_k$ for general intervals $I_i=[L_i,R_i]$.

Similar problem Typical DP Contest, Problem K
(Problem statement translation: a sequence of circles \(C_1,C_2,\ldots,C_k\) are called a target of size \(K\) when \(C_{i+1}\) lies strictly inside \(C_i\) for all \(i\). There are \(N\) circles; circle \(i\) is centered at \((x_i,0)\) and has radius \(r_i\). Find the maximum size of a target consisting of some of these circles.)

Latter case

We exhaustively search for a “separation point” for the two nested intervals. That is, we find for each \(X\), the maximum number of nested intervals contained in \((-\infty,X]\), and the maximum number of nested intervals contained in \((X,\infty)\).

For \(X\), we only need to consider \(R_i\).

Proof

Let \(R_0=-\infty, R_{N+1}=\infty\) for convenience. Take an arbitrary \(X\), and take the \(k\) satisfying \(R_k \leq X < R_{k+1}\). Then, the set of intervals contained in \((-\infty,X]\) is the same as that for \((-\infty,R_k]\). Meanwhile, the set of intervals contained in \((X,\infty)\) is a subset of those for \((R_k,\infty)\). Hence, the sum of “the maximum number of nested intervals contained in \((-\infty,R_k]\)” and “the maximum number of nested intervals contained in \((R_k,\infty)\)” is always greater than or equal to the sum of “the maximum number of nested intervals contained in \((-\infty,X]\)” and “the maximum number of nested intervals contained in \((X,\infty)\).”

Among many ways to find the aforementioned length of a longest decreasing subsequence, let us consider a DP (Dynamic Programming) with

\(\mathrm{dp}_i[x]=\) the length of a longest decreasing subsequence ending with \(x\) among the first \(i\) elements

which will be updated in place using a segment tree. Then, the maximum number of nested intervals contained in \((-\infty,R_i]\) can be obtained as \(\max_x\mathrm{dp}_i[x]\), and that for \((R_i,\infty)\) as \(\max_{x> R_i}\mathrm{dp}_{N}[x]\). This can be evaluated for an additional cost of \(O(N\log N)\) during the process of finding the longest decreasing subsequence.

Therefore, the problem has shown to be solvable in a total of \(O(N\log N)\) time.

Writer’s solution (C++)

#include<bits/stdc++.h>
#include<atcoder/segtree>
using namespace std;

using S=int;
S op(S x,S y){return max(x,y);}
S e(){return 0;}

int main(){
	int n;
	cin >> n;
	vector<array<int,2>>rl;
	for(int i=0;i<n;i++){
		int l,r;
		cin >> l >> r;
		l--,r--;
		if(l>r)swap(l,r);
		rl.push_back({r,l});
	}

	sort(rl.begin(),rl.end());
	atcoder::segtree<S,op,e>seg(2*n);
	
	vector<int>ans(n);
	for(int i=0;i<n;i++){
		auto[r,l]=rl[i];
		ans[i]=seg.prod(l,r)+1;
		seg.set(l,ans[i]);
	}

	for(int i=0;i<n;i++){
		auto[r,l]=rl[i];
		ans[i]+=seg.prod(r,2*n);
	}
	
	cout << *max_element(ans.begin(),ans.end()) << endl;
}