 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
H 行 W 列のマス目があります。 上から i 行目 (1\leq i\leq H)、左から j 列目 (1\leq j\leq W) のマスをマス (i,j) と呼ぶことにします。
マス (i,j)\ (1\leq i\leq H,1\leq j\leq W) には整数 A _ {i,j} が書かれています。
このマス目にドミノを 0 個以上置きます。 1 つのドミノは隣り合う 2 つのマス、つまり
- 1\leq i\leq H,1\leq j\lt W に対するマス (i,j) とマス (i,j+1)
- 1\leq i\lt H,1\leq j\leq W に対するマス (i,j) とマス (i+1,j)
のどれかに置くことができます。
ただし、同じマスに対して複数のドミノを置くことはできません。
ドミノの置き方に対して、置き方のスコアをドミノが置かれていないマスに書かれた整数すべての和として定めます。
ドミノの置き方のスコアとしてありうる最大値を求めてください。
制約
- 1\leq H
- 1\leq W
- HW\leq2000
- -10 ^ {12}\leq A _ {i,j}\leq10 ^ {12}\ (1\leq i\leq H,1\leq j\leq W)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
出力
答えを出力せよ。
入力例 1
3 4 3 -1 -4 1 -5 9 -2 -6 -5 3 -5 8
出力例 1
23
与えられたマス目は以下のようになります。
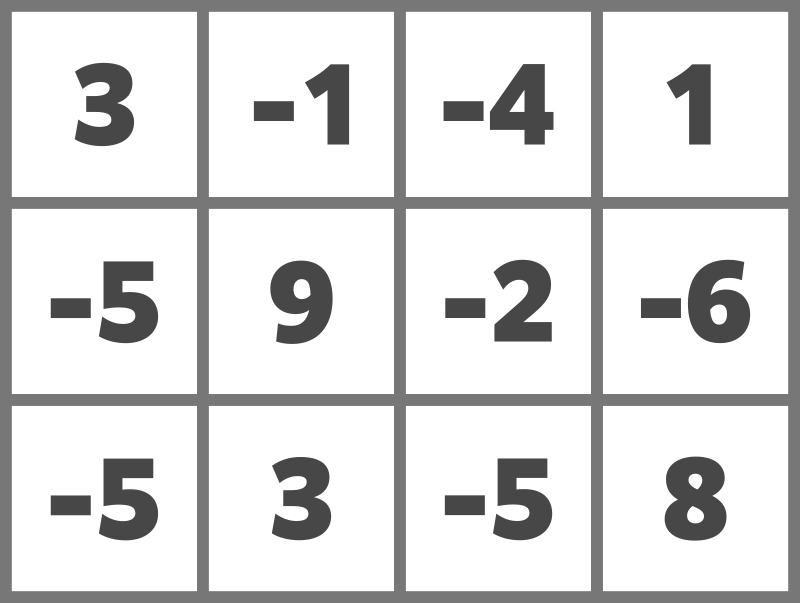
例えば、次のようにドミノを置くことでスコアを 23 とすることができます。
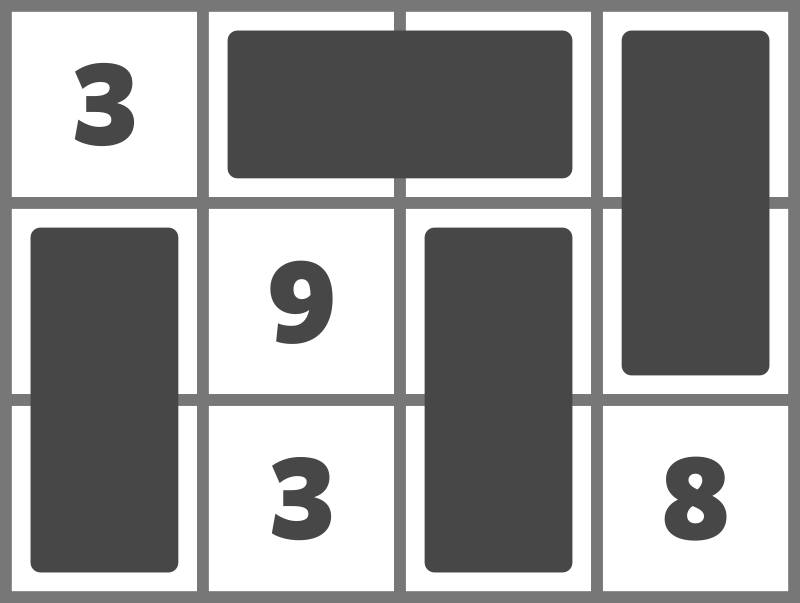
スコアを 24 以上にすることはできないため、23 を出力してください。
入力例 2
5 5 -70 11 -45 -54 -30 -99 39 -83 -69 -77 -48 -21 -43 -96 -24 -54 -65 21 -88 -44 -90 -33 -67 -29 -62
出力例 2
39
入力例 3
8 9 -74832 16944 58683 32965 97236 -52995 43262 -51959 40883 -58715 13846 24919 65627 -11492 -63264 29966 -98452 -75577 40415 77202 15542 -50602 83295 85415 -35304 46520 -38742 37482 56721 -38521 63127 55608 95115 42893 10484 70510 53019 40623 25885 -10246 70973 32528 -33423 19322 52097 79880 74931 -58277 -33783 91022 -53003 11085 -65924 -63548 78622 -77307 81181 46875 -81091 63881 11160 -82217 -55492 62770 39530 -95923 92440 -69899 77737 89392 -14281 84899
出力例 3
2232232
Score : 600 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top (1\leq i\leq H) and the j-th column from the left (1\leq j\leq W).
Cell (i,j)\ (1\leq i\leq H,1\leq j\leq W) has an integer A_{i,j} written on it.
Let us place zero or more dominoes on the grid. A domino covers two adjacent cells, namely one of the following pairs:
- cells (i,j) and (i,j+1) for 1\leq i\leq H,1\leq j\lt W;
- cells (i,j) and (i+1,j) for 1\leq i\lt H,1\leq j\leq W.
No cell may be covered by more than one domino.
For a placement of dominoes, define its score as the sum of all integers written in cells not covered by any domino.
Find the maximum possible score.
Constraints
- 1\leq H
- 1\leq W
- HW\leq2000
- -10 ^ {12}\leq A _ {i,j}\leq10 ^ {12}\ (1\leq i\leq H,1\leq j\leq W)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
Output
Output the answer.
Sample Input 1
3 4 3 -1 -4 1 -5 9 -2 -6 -5 3 -5 8
Sample Output 1
23
The grid is as follows:

For example, the placement below yields a score of 23.

No placement achieves a score of 24 or higher, so output 23.
Sample Input 2
5 5 -70 11 -45 -54 -30 -99 39 -83 -69 -77 -48 -21 -43 -96 -24 -54 -65 21 -88 -44 -90 -33 -67 -29 -62
Sample Output 2
39
Sample Input 3
8 9 -74832 16944 58683 32965 97236 -52995 43262 -51959 40883 -58715 13846 24919 65627 -11492 -63264 29966 -98452 -75577 40415 77202 15542 -50602 83295 85415 -35304 46520 -38742 37482 56721 -38521 63127 55608 95115 42893 10484 70510 53019 40623 25885 -10246 70973 32528 -33423 19322 52097 79880 74931 -58277 -33783 91022 -53003 11085 -65924 -63548 78622 -77307 81181 46875 -81091 63881 11160 -82217 -55492 62770 39530 -95923 92440 -69899 77737 89392 -14281 84899
Sample Output 3
2232232