 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のマス目があります。 上から i 行目 (1\leq i\leq H)、左から j 列目 (1\leq j\leq W) のマスをマス (i,j) と呼ぶことにします。
マス (i,j)\ (1\leq i\leq H,1\leq j\leq W) には非負整数 A _ {i,j} が書かれています。
このマス目にドミノを 0 個以上置きます。 1 つのドミノは隣り合う 2 つのマス、つまり
- 1\leq i\leq H,1\leq j\lt W に対するマス (i,j) とマス (i,j+1)
- 1\leq i\lt H,1\leq j\leq W に対するマス (i,j) とマス (i+1,j)
のどれかに置くことができます。
ただし、同じマスに対して複数のドミノを置くことはできません。
ドミノの置き方に対して、置き方のスコアをドミノが置かれていないマスに書かれた整数すべてのビットごとの排他的論理和として定めます。
ドミノの置き方のスコアとしてありうる最大値を求めてください。
ビットごとの排他的論理和とは
非負整数 A, B のビットごとの排他的論理和 A \oplus B は、以下のように定義されます。
- A \oplus B を二進表記した際の 2^k (k \geq 0) の位の数は、A, B を二進表記した際の 2^k の位の数のうち一方のみが 1 であれば 1、そうでなければ 0 である。
一般に k 個の非負整数 p_1, p_2, p_3, \dots, p_k のビット単位 \mathrm{XOR} は (\dots ((p_1 \oplus p_2) \oplus p_3) \oplus \dots \oplus p_k) と定義され、これは p_1, p_2, p_3, \dots, p_k の順番によらないことが証明できます。
制約
- 1\leq H
- 1\leq W
- HW\leq20
- 0\leq A _ {i,j}\lt 2 ^ {60}\ (1\leq i\leq H,1\leq j\leq W)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
出力
答えを出力せよ。
入力例 1
3 4 1 2 3 8 4 0 7 10 5 2 4 2
出力例 1
15
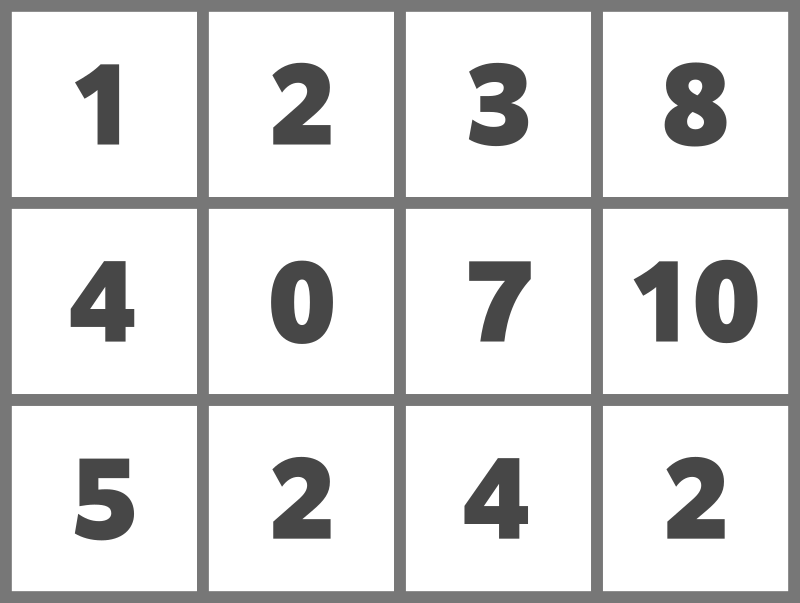
与えられたマス目は以下のようになります。
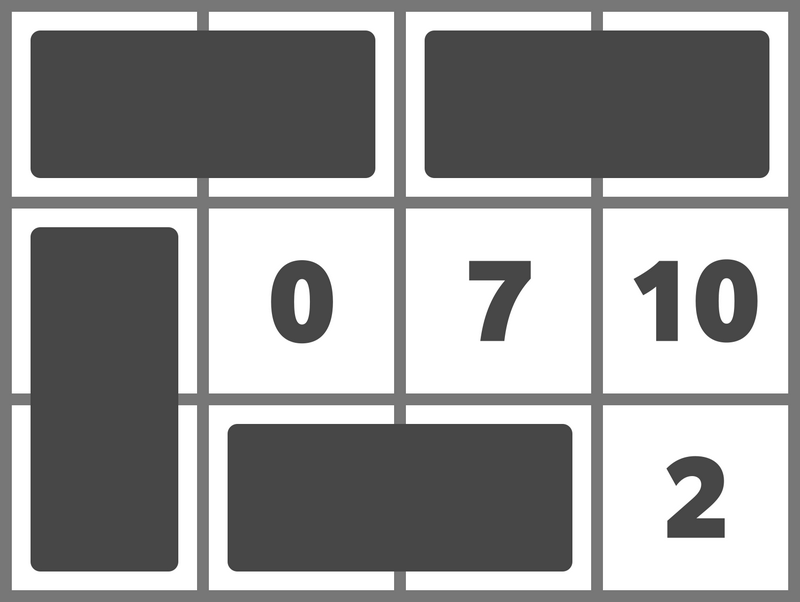
例えば、次のようにドミノを置くことでスコアを 15 とすることができます。
スコアを 16 以上にすることはできないため、15 を出力してください。
入力例 2
1 11 1 2 4 8 16 32 64 128 256 512 1024
出力例 2
2047
ドミノを 1 枚も置かないこともできます。
入力例 3
4 5 74832 16944 58683 32965 97236 52995 43262 51959 40883 58715 13846 24919 65627 11492 63264 29966 98452 75577 40415 77202
出力例 3
131067
Score : 425 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top (1\leq i\leq H) and the j-th column from the left (1\leq j\leq W).
Cell (i,j)\ (1\leq i\leq H,1\leq j\leq W) has a non-negative integer A_{i,j} written on it.
Let us place zero or more dominoes on the grid. A domino covers two adjacent cells, namely one of the following pairs:
- cells (i,j) and (i,j+1) for 1\leq i\leq H,1\leq j\lt W;
- cells (i,j) and (i+1,j) for 1\leq i\lt H,1\leq j\leq W.
No cell may be covered by more than one domino.
For a placement of dominoes, define its score as the bitwise XOR of all integers written in cells not covered by any domino.
Find the maximum possible score.
What is bitwise XOR?
For non-negative integers A and B, their bitwise XOR A \oplus B is defined as follows:
- In binary, the 2^k bit (k \ge 0) of A \oplus B is 1 if exactly one of A and B has 1 in that bit, and 0 otherwise.
For k non-negative integers p_1, p_2, p_3, \dots, p_k, their bitwise XOR is (\dots ((p_1 \oplus p_2) \oplus p_3) \oplus \dots \oplus p_k), which can be proved to be independent of the order of the operands.
Constraints
- 1 \le H
- 1 \le W
- HW \le 20
- 0 \le A_{i,j} < 2^{60} (1 \le i \le H,\ 1 \le j \le W)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W
A _ {1,1} A _ {1,2} \ldots A _ {1,W}
A _ {2,1} A _ {2,2} \ldots A _ {2,W}
\vdots
A _ {H,1} A _ {H,2} \ldots A _ {H,W}
Output
Output the answer.
Sample Input 1
3 4 1 2 3 8 4 0 7 10 5 2 4 2
Sample Output 1
15
The grid is as follows:

For example, the placement below yields a score of 15.

No placement achieves a score of 16 or higher, so output 15.
Sample Input 2
1 11 1 2 4 8 16 32 64 128 256 512 1024
Sample Output 2
2047
You may also choose to place no dominoes.
Sample Input 3
4 5 74832 16944 58683 32965 97236 52995 43262 51959 40883 58715 13846 24919 65627 11492 63264 29966 98452 75577 40415 77202
Sample Output 3
131067