フルーツ列（\(\{ \mathtt{0}, \mathtt{1}, \mathtt{2}, \mathtt{3} \}\)-列）の代わりに\(\{ \mathtt{0}, \mathtt{1} \}\)-列を数え上げる方針です。

フルーツ列から\(\{ \mathtt{0}, \mathtt{1}, \mathtt{2}, \mathtt{3} \}\)-列への置き換え

ダイエットのため、次のようにフルーツを整数に置き換えます。

• リンゴ → \(\mathtt{0}\)
• オレンジ → \(\mathtt{1}\)
• バナナ → \(\mathtt{2}\)
• ブドウ → \(\mathtt{3}\)

すると、これらがそれぞれ \(A, B, C, D\) 回登場する列であって、次の条件を満たすものの個数が答えです。

• 条件 1: \(\mathtt{0}\) はすべて、\(\mathtt{2}\) より先に登場する。
• 条件 2: \(\mathtt{0}\) はすべて、\(\mathtt{3}\) より先に登場する。
• 条件 3: \(\mathtt{1}\) はすべて、\(\mathtt{3}\) より先に登場する。

たとえば入力例 1 では、次の \(5\) 通りの並べ方が条件を満たします。

• \(\mathtt{0123}\)
• \(\mathtt{0132}\)
• \(\mathtt{0213}\)
• \(\mathtt{1023}\)
• \(\mathtt{1032}\)

\(\{ \mathtt{0}, \mathtt{1} \}\)-列への置き換え

さらなるダイエットのため、\(\mathtt{0}, \mathtt{2}\) をともに \(\mathtt{0}\) に、また \(\mathtt{1}, \mathtt{3}\) をともに \(\mathtt{1}\) に置き換えましょう。（つまり、\(2\) で割ったあまりに置き換えます。）

この操作は単射的です。なぜならば条件 1 より\(\mathtt{0}\) のうちはじめの \(A\) 個は \(\mathtt{0}\) 由来、残りの \(C\) 個は \(\mathtt{2}\) 由来であることが確定し、条件 3より \(\mathtt{1}\) のうちはじめの \(B\) 個は \(\mathtt{1}\) 由来、残りの \(D\) 個は \(\mathtt{3}\) 由来であることが確定するからです。

たとえば入力例 1 の \(5\) 通りの並べ方は、次の \(\mathtt{0}\)-\(\mathtt{1}\) 列に写ります。

• \(\mathtt{0101}\)
• \(\mathtt{0110}\)
• \(\mathtt{0011}\)
• \(\mathtt{1001}\)
• \(\mathtt{1010}\)

\(\{ \mathtt{0}, \mathtt{1} \}\)-列の満たすべき条件

条件 2 に着目すると、\(\mathtt{0}, \mathtt{1}\) がそれぞれ \(A + C, B + D\) 回登場する列であって、次の条件を満たすものの個数が答えであることがわかります。

• 条件 2’: 先頭 \(A + B\) 項に、\(\mathtt{0}\) が \(A\) 個以上ある

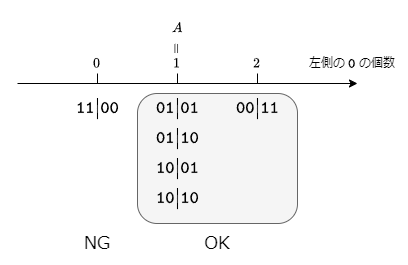
答え

先頭 \(A + B\) 項のうち、ダミー変数 \(i\) を用いて \(\mathtt{0}\) が \(A + i\) 個あると場合分けして足し合わせることで、次の答えを得ます。

\[ \sum_{i \ge 0} \binom{A + B}{A + i} \binom{C + D}{C - i} \]