Prerequisite: Trie

This problem is an exercise of trie, which is a data structure that represents a list of strings as a rooted tree. Information stored on each vertex allows us efficient manipulations regarding prefixes.

A trie is constructed so that each vertex represents a character, and a path from the root to another vertex corresponds to a string. Strings with common prefixes share a path from the root to some of their ancestor.

Each vertex of the trie maintain the following information:

• The character represented by the vertex
• The list of children of the vertex
• The list of strings that is accepted at the vertex; i.e. the list of indices of the original list, that coincides with the string represented by the path from the root to the vertex

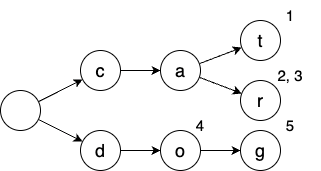
For example, a list of strings \((S_1,S_2,S_3,S_4,S_5)=(\texttt{cat},\texttt{car},\texttt{car},\texttt{do},\texttt{dog})\) is represented by the following trie. The numbers on the top left of each vertex represent the indices of the string that is accepted by the vertex.

Solution of the problem

We describe how to solve the problem using a trie. We maintain all the given strings \(S_i\) in a single trie \(T\), regardless of which of \(X\) and \(Y\) it will belong to. Also, maintain a set \(Z\), which stores “the strings \(S_i\) contained in \(Y\) that has an element \(S_j\) in \(X\) as a prefix.” The sought answer is \(|Y| - |Z|\). If we can update \(Z\) fast enough every time \(S_i\) is given, then the problem can be solved.

There are two possible situations where an element is added to \(Z\):

1. Query \(1\) asks to add \(S_i\) to \(X\), causing \(S_j \in Y \; (j<i)\) to have \(S_i\) as a prefix, resulting in \(S_j\) being added to \(Z\).
2. Query \(2\) asks to add \(S_i\) to \(Y\), causing \(S_i\) to have \(S_j \in X \; (j<i)\) as a prefix, resulting in \(S_i\) being added to \(Z\).

We explain how to handle each type of query.

Processing query 1

If the subtree rooted at the vertex accepting \(S_i \in X\) contains a vertex that accepts \(S_j \in Y\), then we add \(S_j\) to \(Z\).

If we inspect all the vertices in the subtree, we cannot make it within the execution time limit. Instead, we will keep for each vertex \(v\) in \(T\), the set of the elements \(S_j\in Y\) to be added to \(Z\) when an \(S_i\in X\) accepted by \(v\) is added for the next time. This can be updated by, every time adding \(S_j \in Y\) to \(T\), for all vertex \(v\) that accepts a prefix of \(S_j\), adding \(S_j\) to \(Z_v\). When adding \(S_i\in X\), add all \(j\in Z_v\) to \(Z\) and empty \(Z_v\), where \(v\) is the vertex accepting \(S_i\). Since \(Z_v\) can have up to \(Q\) elements, so it seems inefficient at a glance, but the total number of times that an \(S_j\) is taken out of any \(Z_v\) is at most \(S_j\) times. Therefore, the overall time complexity is \(O( \sum_{i=1}^Q |S_i| \log Q)\).

Processing query 2

It is sufficient to check if there is a vertex \(v\) that accepts a prefix of \(S_i \in X\) and also accepts an \(S_j \in X\). To this end, we maintain a flag \(f_v\) for each vertex \(v\) in \(T\) signifying whether \(X\) contains a string that is accepted by that vertex. When adding a string of \(X\) to \(T\), we set \(f_v=\mathrm{true}\) for the vertex \(v\) accepting that string; when adding a string of \(Y\), we check if there exists an ancestor \(v\) of the vertex that accepts its prefix such that \(f_v=\mathrm{true}\).

Summary

To wrap up, each type of query can be processed as follows:

• When adding \(S_i\) to \(X\):
  • Add \(S_i\) to \(T\).
  • For the vertex \(v\) accepting \(S_i\), perform the following:
    • Add each \(S_j\in Z_v\) to \(Z\), and empty \(Z_v\).
    • Let \(f_v=\mathrm{true}\).
• When adding \(S_i\) to \(Y\):
  • Add \(S_i\) to \(T\).
  • For each vertex \(v\) accepting a prefix of \(S_i\), perform the following:
    • Add \(i\) to \(Z_v\).
    • If \(f_v=\mathrm{true}\), add \(i\) to \(Z\).

The overall time complexity is \(O(\sum_{i=1}^Q |S_i| \log Q)\).

Sample code (Python)