D - Line Crossing Editorial /

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 400 点

問題文

円周上に N 個の点が等間隔に並んでおり、時計回りに 1,2,\ldots,N と番号がつけられています。

M 本の相異なる直線があり、i 本目の直線は異なる 2 つの点、点 A_i と点 B_i を通る直線です。(1 \leq i \leq M)

以下の 2 つの条件をともに満たすような整数の組 (i,j) の個数を求めてください。

  • 1 \leq i < j \leq M
  • i 本目の直線と j 本目の直線は交わる

制約

  • 2 \leq N \leq 10^6
  • 1 \leq M \leq 3 \times 10^{5}
  • 1 \leq A_i < B_i \leq N (1 \leq i \leq M)
  • (A_i,B_i) \neq (A_j,B_j) (i \neq j)
  • 入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M

出力

答えを出力せよ。

入力例 1

8 3
1 5
1 8
2 4

出力例 1

2

次の図のように円周上に 8 個の点と 3 本の直線があります。

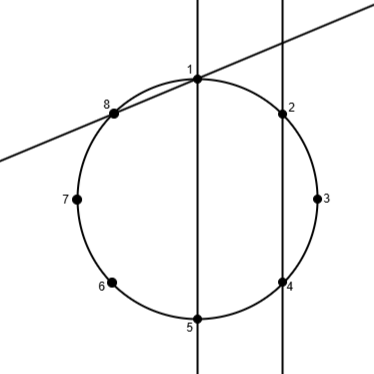
1 本目の直線と 2 本目の直線は交わります。1 本目の直線と 3 本目の直線は交わりません。2 本目の直線と 3 本目の直線は交わります。(i,j)=(1,2),(2,3) の 2 つの組が条件を満たすため、2 を出力します。

入力例 2

5 10
2 5
1 5
1 2
2 4
2 3
1 3
1 4
3 5
3 4
4 5

出力例 2

40

Score : 400 points

Problem Statement

There are N equally spaced points on a circle labeled clockwise as 1,2,\ldots,N.

There are M distinct lines, where the i-th line passes through two distinct points A_i and B_i (1 \leq i \leq M).

Find the number of pairs (i,j) satisfying:

  • 1 \le i < j \le M, and
  • the i-th and j-th lines intersect.

Constraints

  • 2 \leq N \leq 10^6
  • 1 \leq M \leq 3 \times 10^{5}
  • 1 \leq A_i < B_i \leq N (1 \leq i \leq M)
  • (A_i,B_i) \neq (A_j,B_j) (i \neq j)
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M

Output

Print the answer.

Sample Input 1

8 3
1 5
1 8
2 4

Sample Output 1

2

As shown in the diagram below, there are eight points and three lines on the circle.

The 1st and 2nd lines intersect. The 1st and 3rd lines do not intersect. The 2nd and 3rd lines intersect. Since the pairs (i,j)=(1,2),(2,3) satisfy the conditions, print 2.

Sample Input 2

5 10
2 5
1 5
1 2
2 4
2 3
1 3
1 4
3 5
3 4
4 5

Sample Output 2

40