 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
無限に広い 2 次元グリッドがあり、このグリッドの座標 (0,0) に焚き火があります。
時刻 t=0 では、マス (0,0) にのみ煙が存在します。
N, W, S, E からなる長さ N の文字列 S が与えられ、時刻 t=1,2,\dots,N では次の現象が順番に発生します。
- 風が吹き、現時点で存在する全ての煙が以下の通りに移動する。
- S の t 文字目が
Nであるとき、マス (r,c) にある煙がマス (r-1,c) に移動する。 - S の t 文字目が
Wであるとき、マス (r,c) にある煙がマス (r,c-1) に移動する。 - S の t 文字目が
Sであるとき、マス (r,c) にある煙がマス (r+1,c) に移動する。 - S の t 文字目が
Eであるとき、マス (r,c) にある煙がマス (r,c+1) に移動する。
- S の t 文字目が
- マス (0,0) に煙が存在しない場合、新たな煙がマス (0,0) に生成される。
高橋君はマス (R,C) に立っています。
整数 1 \le t \le N について、時刻 t+0.5 においてマス (R,C) に煙が存在するか判定し、出力欄の形式に従って出力してください。
制約
- N は 1 以上 200000 以下の整数
- S は
N,W,S,Eからなる長さ N の文字列 - R,C は -N 以上 N 以下の整数
- (R,C) \neq (0,0)
入力
入力は以下の形式で標準入力から与えられる。
N R C S
出力
答えを N 文字の 0, 1 からなる文字列として出力せよ。
出力する文字列のうち t 文字目 (1 \le t \le N) は次の通りにせよ。
- 時刻 t+0.5 においてマス (R,C) に煙が存在するなら
1 - 時刻 t+0.5 においてマス (R,C) に煙が存在しないなら
0
入力例 1
6 -2 1 NNEEWS
出力例 1
001010
時刻 1.5,2.5,4.5,6.5 ではマス (-2,1) には煙が存在せず、時刻 3.5,5.5 ではマス (-2,1) に煙が存在します。
よって、 001010 と出力します。
図では焚き火のあるマス (0,0) を基準として、マス (r,c) を
- r < 0 なら -r マス上に
- r \ge 0 なら r マス下に
- c < 0 なら -c マス左に
- c \ge 0 なら c マス右に
描画します。
時刻 0.5 でのグリッドの状態は次の通りです。
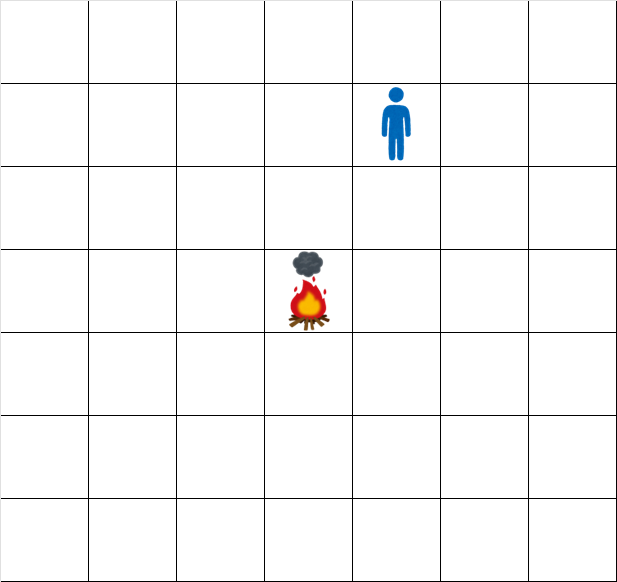
時刻 1.5 でのグリッドの状態は次の通りです。
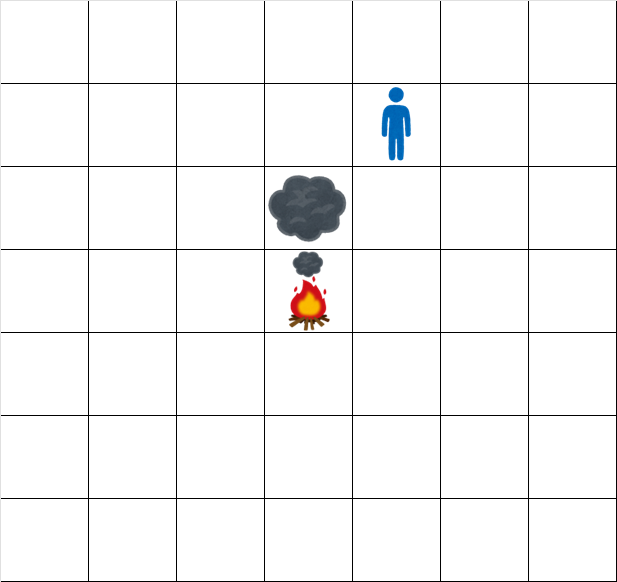
時刻 2.5 でのグリッドの状態は次の通りです。
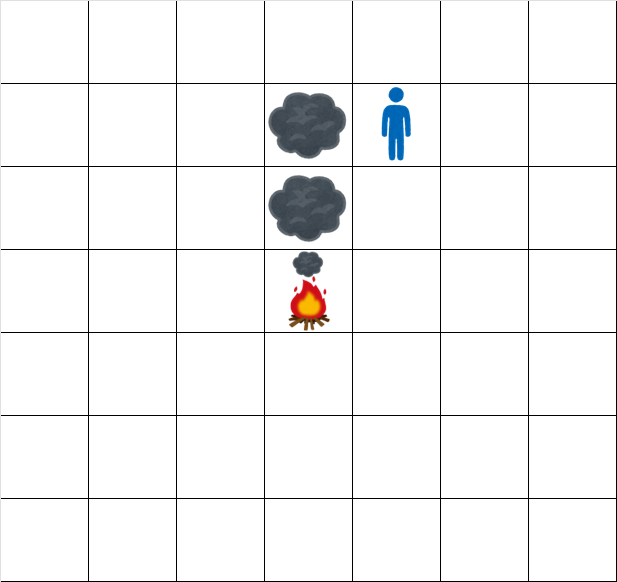
時刻 3.5 でのグリッドの状態は次の通りです。
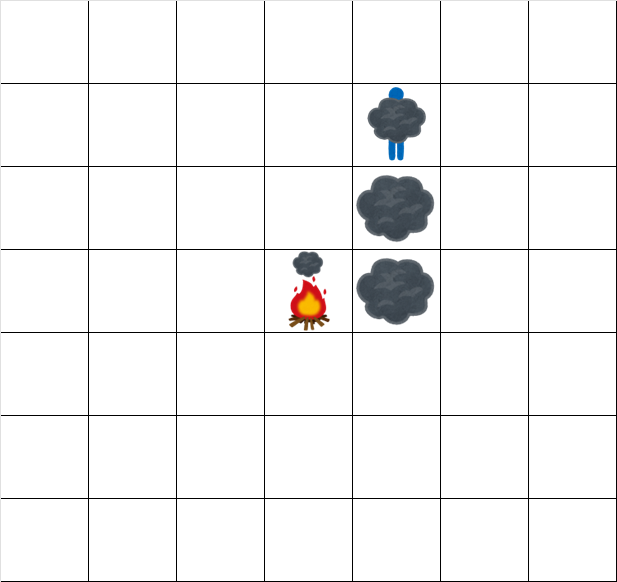
時刻 4.5 でのグリッドの状態は次の通りです。
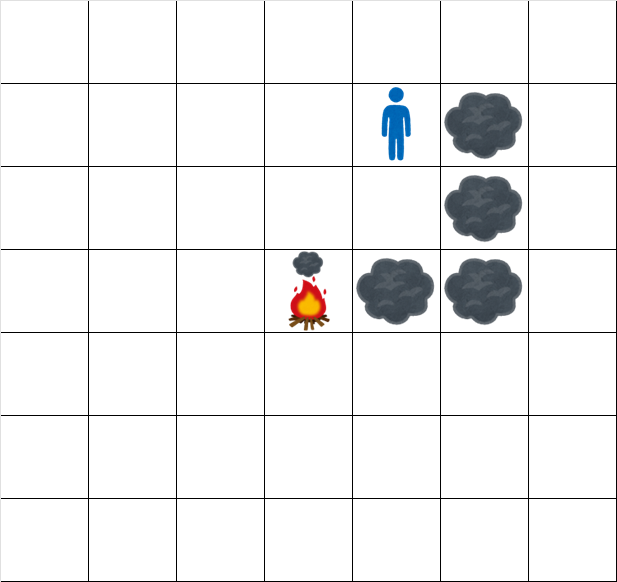
時刻 5.5 でのグリッドの状態は次の通りです。
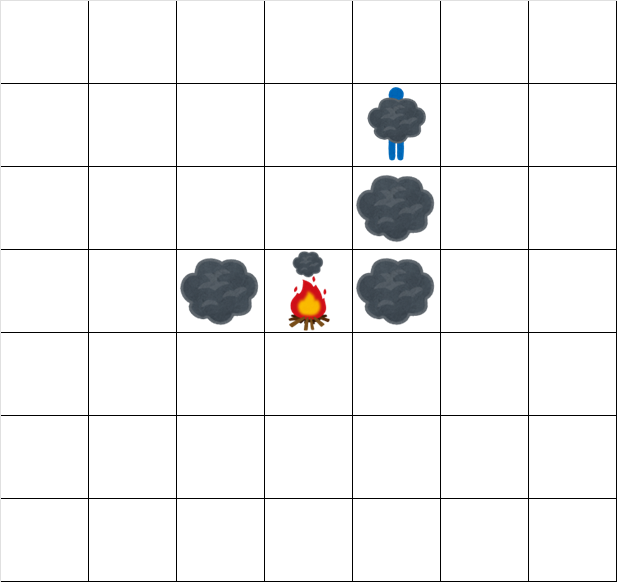
時刻 6.5 でのグリッドの状態は次の通りです。
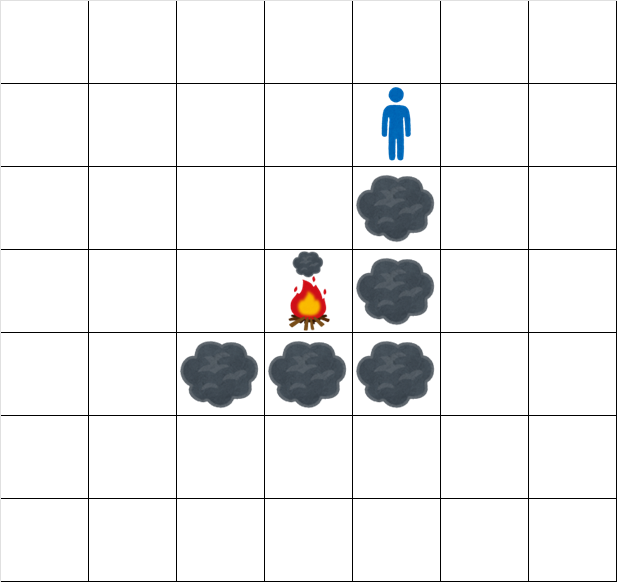
入力例 2
10 1 2 NEESESWEES
出力例 2
0001101011
入力例 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
出力例 3
00100111111000101111
Score : 425 points
Problem Statement
There is an infinitely large two-dimensional grid, with a campfire at coordinate (0,0).
At time t=0, smoke exists only at cell (0,0).
You are given a length-N string S consisting of N, W, S, E. At times t=1,2,\dots,N, the following happen in order:
- Wind blows, and all the smoke present at that time moves as follows:
- If the t-th character of S is
N, smoke in cell (r,c) moves to cell (r-1,c). - If it is
W, smoke in cell (r,c) moves to cell (r,c-1). - If it is
S, smoke in cell (r,c) moves to cell (r+1,c). - If it is
E, smoke in cell (r,c) moves to cell (r,c+1).
- If the t-th character of S is
- If there is no smoke in cell (0,0), new smoke is generated at cell (0,0).
Takahashi is standing at cell (R,C).
For each integer 1 \le t \le N, determine if smoke exists at cell (R,C) at time t+0.5, and print the response according to the required format.
Constraints
- N is an integer between 1 and 200000, inclusive.
- S is a length N string consisting of
N,W,S,E. - R and C are integers between -N and N, inclusive.
- (R,C) \neq (0,0)
Input
The input is given from Standard Input in the following format:
N R C S
Output
Print an N-character string consisting of 0 and 1.
The t-th character (1 \le t \le N) should be:
1if smoke exists at cell (R,C) at time t+0.5, and0otherwise.
Sample Input 1
6 -2 1 NNEEWS
Sample Output 1
001010
At times 1.5,2.5,4.5,6.5, there is no smoke at cell (-2,1). At times 3.5,5.5, there is smoke at cell (-2,1).
Hence, output 001010.
In the figures below, taking cell (0,0) with the campfire as a reference, cell (r,c) is drawn:
- -r cells up if r < 0,
- r cells down if r \ge 0,
- -c cells left if c < 0,
- c cells right if c \ge 0.
The grid at time 0.5 looks like:

The grid at time 1.5 looks like:

The grid at time 2.5 looks like:

The grid at time 3.5 looks like:

The grid at time 4.5 looks like:

The grid at time 5.5 looks like:

The grid at time 6.5 looks like:

Sample Input 2
10 1 2 NEESESWEES
Sample Output 2
0001101011
Sample Input 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
Sample Output 3
00100111111000101111