 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
H 行 W 列のグリッドがあります。 上から i 行目、左から j 列目のマスを (i,j) と表記します。
各マスはスタートマス・ゴールマス・空きマス・障害物マスのいずれかであり、その情報は H 個の長さ W の文字列 S_1,S_2,\dots,S_H によって表されます。
具体的には、マス (i,j) は S_i の j 文字目が S であるときスタートマス、G であるときゴールマス、. であるとき空きマス、# であるとき障害物マスです。
ここで、スタートマスとゴールマスはちょうど 1 つずつ存在することが保証されます。
あなたは今スタートマスにいます。 あなたの目標は、今いるマスと辺で隣接するマスに移動することを繰り返してゴールマスへ行くことです。 ただし、障害物マスやグリッドの外に移動することはできず、また縦移動と横移動を 1 回ずつ交互に行わなければなりません。(最初の移動の向きは任意です。)
ゴールマスへ行くことが可能であるか判定し、可能ならば移動回数の最小値を求めてください。
より形式的には、以下の条件をすべて満たすマスの列 (i_1,j_1),(i_2,j_2),\dots,(i_k,j_k) が存在するか判定し、存在するならば k-1 の最小値を求めてください。
- すべての 1\leq l\leq k について、1\leq i_l\leq H かつ 1\leq j_l\leq W であり、(i_l,j_l) は障害物マスでない
- (i_1,j_1) はスタートマス
- (i_k,j_k) はゴールマス
- すべての 1\leq l\leq k-1 について、|i_l-i_{l+1}|+|j_l-j_{l+1}|=1
- すべての 1\leq l\leq k-2 について、i_l\neq i_{l+1} ならば i_{l+1}=i_{l+2}
- すべての 1\leq l\leq k-2 について、j_l\neq j_{l+1} ならば j_{l+1}=j_{l+2}
制約
- 1\leq H,W \leq 1000
- H,W は整数
- S_i は
S,G,.,#からなる長さ W の文字列 - スタートマスとゴールマスはちょうど 1 つずつ存在する
入力
入力は以下の形式で標準入力から与えられる。
H W S_1 S_2 \vdots S_H
出力
ゴールマスへ行くことが可能ならば移動回数の最小値を、不可能ならば -1 を出力せよ。
入力例 1
3 5 .S#.G ..... .#...
出力例 1
7
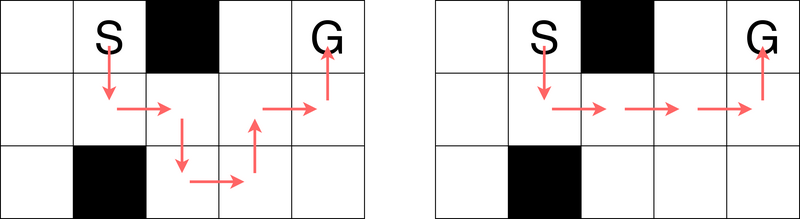
左図のように (1,2)\rightarrow(2,2)\rightarrow(2,3)\rightarrow(3,3)\rightarrow(3,4)\rightarrow(2,4)\rightarrow(2,5)\rightarrow(1,5) と移動することで、7 回の移動でゴールマスへ行くことができます。 6 回以下の移動でゴールマスへ行くことはできないので、答えは 7 です。
右図のように横移動を連続で行う経路(あるいは縦移動を連続で行う経路)はとれないことに注意してください。
入力例 2
3 5 ..#.G ..... S#...
出力例 2
-1
ゴールマスへ行くことはできません。
入力例 3
8 63 ............................................................... ..S...#............................#####..#####..#####..####G.. ..#...#................................#..#...#......#..#...... ..#####..####...####..####..#..#...#####..#...#..#####..#####.. ..#...#..#..#...#..#..#..#..#..#...#......#...#..#..........#.. ..#...#..#####..####..####..####...#####..#####..#####..#####.. ................#.....#........#............................... ................#.....#........#...............................
出力例 3
148
Score : 400 points
Problem Statement
You are given a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
Each cell is one of the following: a start cell, a goal cell, an empty cell, or an obstacle cell. This information is described by H strings S_1,S_2,\dots,S_H, each of length W. Specifically, the cell (i,j) is a start cell if the j-th character of S_i is S, a goal cell if it is G, an empty cell if it is ., and an obstacle cell if it is #. It is guaranteed that there is exactly one start cell and exactly one goal cell.
You are currently on the start cell. Your objective is to reach the goal cell by repeatedly moving to a cell adjacent by an edge to the one you are in. However, you cannot move onto an obstacle cell or move outside the grid, and you must alternate between moving vertically and moving horizontally each time. (The direction of the first move can be chosen arbitrarily.)
Determine if it is possible to reach the goal cell. If it is, find the minimum number of moves required.
More formally, check if there exists a sequence of cells (i_1,j_1),(i_2,j_2),\dots,(i_k,j_k) satisfying all of the following conditions. If such a sequence exists, find the minimum value of k-1.
- For every 1 \leq l \leq k, it holds that 1 \leq i_l \leq H and 1 \leq j_l \leq W, and (i_l,j_l) is not an obstacle cell.
- (i_1,j_1) is the start cell.
- (i_k,j_k) is the goal cell.
- For every 1 \leq l \leq k-1, |i_l - i_{l+1}| + |j_l - j_{l+1}| = 1.
- For every 1 \leq l \leq k-2, if i_l \neq i_{l+1}, then i_{l+1} = i_{l+2}.
- For every 1 \leq l \leq k-2, if j_l \neq j_{l+1}, then j_{l+1} = j_{l+2}.
Constraints
- 1 \leq H,W \leq 1000
- H and W are integers.
- Each S_i is a string of length W consisting of
S,G,.,#. - There is exactly one start cell and exactly one goal cell.
Input
The input is given from Standard Input in the following format:
H W S_1 S_2 \vdots S_H
Output
If it is possible to reach the goal cell, print the minimum number of moves. Otherwise, print -1.
Sample Input 1
3 5 .S#.G ..... .#...
Sample Output 1
7

As shown in the left figure, you can move as (1,2)\rightarrow(2,2)\rightarrow(2,3)\rightarrow(3,3)\rightarrow(3,4)\rightarrow(2,4)\rightarrow(2,5)\rightarrow(1,5), reaching the goal cell in 7 moves. It is impossible in 6 moves or fewer, so the answer is 7.
Note that you cannot take a path that moves horizontally (or vertically) consecutively without alternating as shown in the right figure.
Sample Input 2
3 5 ..#.G ..... S#...
Sample Output 2
-1
It is not possible to reach the goal cell.
Sample Input 3
8 63 ............................................................... ..S...#............................#####..#####..#####..####G.. ..#...#................................#..#...#......#..#...... ..#####..####...####..####..#..#...#####..#...#..#####..#####.. ..#...#..#..#...#..#..#..#..#..#...#......#...#..#..........#.. ..#...#..#####..####..####..####...#####..#####..#####..#####.. ................#.....#........#............................... ................#.....#........#...............................
Sample Output 3
148