D - Santa Claus 2 解説 /

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 425 点

問題文

2次元平面上の N 点 (X_1,Y_1),\ldots,(X_N,Y_N) に家が建っています。

最初、点 (S_x,S_y) にサンタクロースがいます。サンタクロースは列 (D_1,C_1),\ldots,(D_M,C_M) に従って以下の行動を行います。

  • i=1,2,\ldots,M の順に以下のように移動する。
    • 現在サンタクロースがいる点を (x,y) とする。
      • D_i が U なら、(x,y) から (x,y+C_i) に直線で移動する。
      • D_i が D なら、(x,y) から (x,y-C_i) に直線で移動する。
      • D_i が L なら、(x,y) から (x-C_i,y) に直線で移動する。
      • D_i が R なら、(x,y) から (x+C_i,y) に直線で移動する。

行動を終えたあとにサンタクロースがいる点と、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。

制約

  • 1 \leq N \leq 2\times 10^5
  • 1 \leq M \leq 2\times 10^5
  • -10^9 \leq X_i,Y_i \leq 10^9
  • (X_i,Y_i) は相異なる
  • -10^9 \leq S_x,S_y \leq 10^9
  • (S_x,S_y) に家は建っていない
  • D_i は U, D, L, R のいずれかである
  • 1 \leq C_i \leq 10^9
  • 与えられる数値は全て整数である

入力

入力は以下の形式で標準入力から与えられる。

N M S_x S_y
X_1 Y_1
\vdots
X_N Y_N
D_1 C_1
\vdots
D_M C_M

出力

行動を終えたあとサンタクロースがいる点を (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。

入力例 1

3 4 3 2
2 2
3 3
2 1
L 2
D 1
R 1
U 2

出力例 1

2 3 2

サンタクロースは以下のように行動します。

図

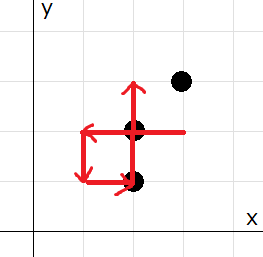
  • D_1= L なので (3,2) から (3-2,2) に直線で移動する。このとき (2,2) に建っている家を通過する。
  • D_2= D なので (1,2) から (1,2-1) に直線で移動する。
  • D_3= R なので (1,1) から (1+1,1) に直線で移動する。このとき (2,1) に建っている家を通過する。
  • D_4= U なので (2,1) から (2,1+2) に直線で移動する。このとき (2,2) に建っている家を通過するが、この家はすでに通過したことがある家である。

行動により通過または到達した家の数は 2 です。

入力例 2

1 3 0 0
1 1
R 1000000000
R 1000000000
R 1000000000

出力例 2

3000000000 0 0

オーバーフローに注意してください。

Score : 425 points

Problem Statement

There are N houses at points (X_1,Y_1),\ldots,(X_N,Y_N) on a two-dimensional plane.

Initially, Santa Claus is at point (S_x,S_y). He will act according to the sequence (D_1,C_1),\ldots,(D_M,C_M) as follows:

  • For i=1,2,\ldots,M in order, he moves as follows:
    • Let (x,y) be the point where he currently is.
      • If D_i is U, move in a straight line from (x,y) to (x,y+C_i).
      • If D_i is D, move in a straight line from (x,y) to (x,y-C_i).
      • If D_i is L, move in a straight line from (x,y) to (x-C_i,y).
      • If D_i is R, move in a straight line from (x,y) to (x+C_i,y).

Find the point where he is after completing all actions, and the number of distinct houses he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.

Constraints

  • 1 \leq N \leq 2\times 10^5
  • 1 \leq M \leq 2\times 10^5
  • -10^9 \leq X_i,Y_i \leq 10^9
  • The pairs (X_i,Y_i) are distinct.
  • -10^9 \leq S_x,S_y \leq 10^9
  • There is no house at (S_x,S_y).
  • Each D_i is one of U, D, L, R.
  • 1 \leq C_i \leq 10^9
  • All input numbers are integers.

Input

The input is given from Standard Input in the following format:

N M S_x S_y
X_1 Y_1
\vdots
X_N Y_N
D_1 C_1
\vdots
D_M C_M

Output

Let (X,Y) be the point where he is after completing all actions, and C be the number of distinct houses passed through or arrived at. Print X,Y,C in this order separated by spaces.

Sample Input 1

3 4 3 2
2 2
3 3
2 1
L 2
D 1
R 1
U 2

Sample Output 1

2 3 2

Santa Claus behaves as follows:

Figure

  • D_1= L, so he moves from (3,2) to (3-2,2) in a straight line. During this, he passes through the house at (2,2).
  • D_2= D, so he moves from (1,2) to (1,2-1) in a straight line.
  • D_3= R, so he moves from (1,1) to (1+1,1) in a straight line. During this, he passes through the house at (2,1).
  • D_4= U, so he moves from (2,1) to (2,1+2) in a straight line. During this, he passes through the house at (2,2), but it has already been passed.

The number of houses he passed or arrived during his actions is 2.

Sample Input 2

1 3 0 0
1 1
R 1000000000
R 1000000000
R 1000000000

Sample Output 2

3000000000 0 0

Be careful with overflow.