\(O(M^{2} + MN\log(N))\) で解く方法です。 マス目の形が特徴的なことを用いています。

マス目が正方形のとき

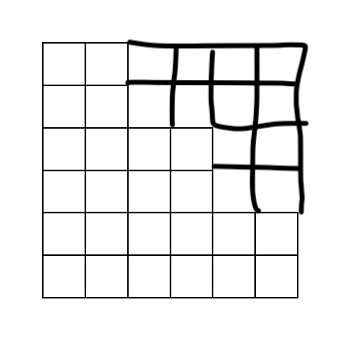
このような形であるときは、解説にもある通り EDPC Y Grid2 と同じ包除原理で解くことができます。

マス目が \(1\) 段の階段のとき

以上のバッテンが入ったマスは入れないと仮定します。これも先ほどと同じように包除原理を用いて解くことができます。なぜなら、あるマスからあるマスへの経路の数は、カタラン数を求めるときの鏡像法と同じように求めることができるからです。関連する ABC の問題

元の問題を解く

準備

\(i = 0, 1, \dots, N\) に対して、\((2i + 1, 2i + 2)\) のマスを角 \(i\) と呼ぶことにします。

壁があるマスとスタート地点とゴール地点の 特殊マス として、index の和が小さい順に 特殊マス \(0,1,\dots M +1\) とし、 \(\text{dp}[i]\) を特殊マス \(i\) に壁がないと仮定したときの、スタート地点から 特殊マス \(i\) までの経路数とします。ただし、包除原理の都合上、\(\text{dp}[0] = -1\) で初期化されます。\(dp[M+1]\) が今回求めたい答えとなります。

\(\text{corner}[i][j]\) を \(k=0,2,\dots ,i - 1\) における、「\(\text{dp}[k]\) と、壁が全てないときの 特殊マス \(k\) から 角 \(i\) までの経路数の積」の総和とします。

説明の途中で「角を通らない」という言葉が出てきますが、これは、「始点と終点以外で角を通らない」と置き換えて読んでください。

また、説明の簡略のため、特殊マスに角マスは含まれないことにします。実装の際は、そのことに注意をした実装をしてください。

dp table の更新

\(\text{dp}[0], \text{dp}[1],\dots ,\text{dp}[i - 1]\) と \(\text{corner}[i]\) が求まっているとします。

\(\text{dp}[i]\) は、 \(k=0,2,\dots ,i - 1\) における、\(k=0,2,\dots ,i - 1\) における、「\(\text{dp}[k]\) と、壁が全てないときの 特殊マス \(k\) から 特殊マス \(i\) までの経路数の積」の総和に \(-1\) をかけたものです。経路を \(2\) 種類に分解して考えます。

• 角を通らないとき

  • 角を通らないかつ壁が全てないときの 特殊マス \(k\) から 特殊マス \(i\) までの経路数は鏡像法で簡単に求まるため、それを求め積を取れば良いです。

• 角を通るとき

  • 最後に通る角を角 \(j\) だとしたら、角を通らないかつ壁が全てないときの、角 \(j\) から 特殊マス \(i\) までの経路数が求まれば、これと \(\text{corner}[i][j]\) の積を取ることで計算できます。角 \(j\) の次は必ずマス\((2i+2,2i+2)\) を通るため、経路数は鏡像法で求めることができます。

corner table の更新

\(\text{corner}[i]\) と \(\text{dp}[i]\) が求まっているときに、 \(\text{corner}[i + 1]\) が求まれば良いです。 つまり、特殊マス \(i\) から角 \(j\) への経路数が求まれば良いです。

ここで、\(x\) に関する多項式 \(f,g,h\) を以下のように定義します。

• \([x^{j}](f(x)) := \) 壁が全てないときの 特殊マス \(i\) から角 \(j\) への経路数
• \([x^{j}](g(x)) := \) 角を通らないかつ壁が全てないときの 特殊マス \(i\) から角 \(j\) への経路数
• \([x^{j}](h(x)) := \) 角を通らないかつ壁が全てないときの 角 \(a\) から角 \(a + j\) への経路数
• ただし、 \([x^{0}](h(x)) = 0\) とする。

すると、以下の式が成り立ちます。

\[f(x) = g(x) + f(x) h(x)\]

\[f(x) = \frac{g(x)}{1 - h(x)}\]

よって、\(g(x),h(x)\) が求まれば畳み込みを用いて \(f(x)\) も求めることができます。これを用いて \(\text{corner}\) を更新すれば良いです。

\(g(x)\) は、角 \(j\) の \(1\) つ前のマスが必ず \((2j + 1, 2j + 1)\) になることから求められます。 \(h(x)\) も同様に求められて、\([x^{j}](h(x)) = \dfrac{(2j+2)!}{(j+1)!(j+2)!}\) が成り立ちます。

まとめ

以上で求めることができました。\(\frac{1}{1 - h(x)}\) は \(h(x)\) がわかっていれば \(N\) 項までは \(O(N\log(N))\) で求めることができます。(Nyaan さんの記事 の逆元の項目を参照)

dp table の更新に \(O(N+M)\) 回の計算が必要なのと、 \(f(x)\) を \(M\) 回求める必要があるため、計算量は \(O(M^{2} + MN\log(N))\) です。

c++ 実装例

• \(h\) を先に変換しておくことで、\(\frac{2}{3}\) 倍の定数倍高速化をしています。
• 特殊マス が角であるときは、特殊マス の後に必ずその角を通ることにしています。例えば、\(g\) は \(x^i\) になります。また、角を通らないそのマスからの別のマスへの経路数は \(0\) になります。テストケースに角に壁があるケースが少ないので、このコードが間違っているかもしれません。手元で \(N\leq 6\) を満たす全てのテストケースで愚直な解と答えが一致していることを確認しています。