不満度の定義式のうち、\(A_i\) または \(B_i\) の部分を不満係数、\(|x-y|\) の部分を偏りと呼びます (すなわち、不満度は不満係数と偏りの積です)。また、犬と猫を合わせて単に動物と呼びます。

1. 最適解の構造

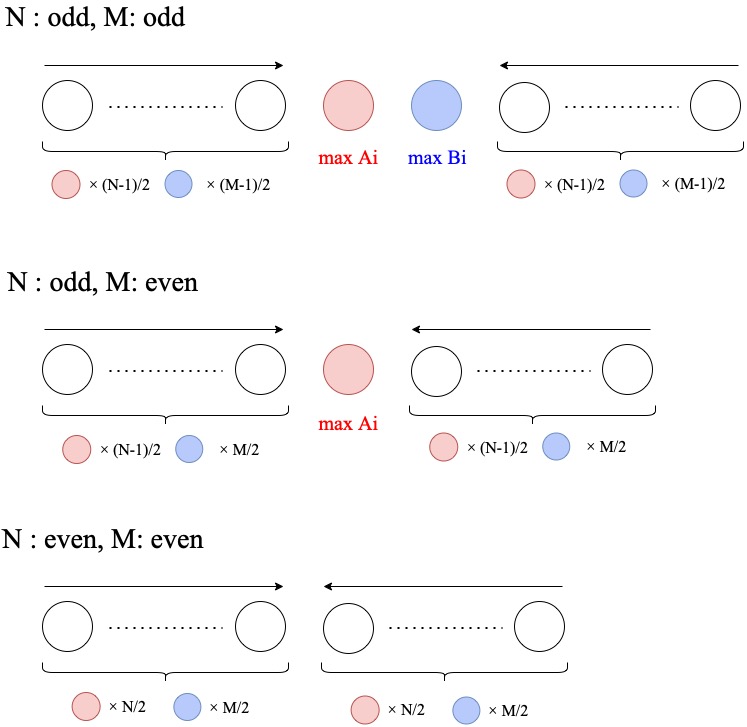
実は、最適解は必ず以下の図のような構造になっています (「\(N\) が偶数、\(M\) が奇数」の場合は「 \(N\) が奇数、\(M\) が偶数」の場合と同様なので扱いません)。

図の説明：赤い丸は犬を、青い丸は猫を、白い丸は犬と猫のいずれかを表しています。また、丸の部分列の上に書かれた矢印は、その部分列内において、矢印の方向に向かって不満係数が昇順となるように並んでいることを意味します。例えば一番上の図は、「\(\frac{N-1}{2}\) 匹の犬と \(\frac{M-1}{2}\) 匹の猫を不満係数の昇順に並べた列」、「\(A_i\) が最大の犬」、「\(B_i\) が最大の猫」、「\(\frac{N-1}{2}\) 匹の犬と \(\frac{M-1}{2}\) 匹の猫を不満係数の降順に並べた列」をこの順に連結したものを表しています。

それぞれのパターンについて最適性を証明していきます。

証明を飛ばしたい方はこちら

\(N\) が奇数、\(M\) が奇数の場合

証明すべき事柄を以下のように分割します。

1. 中央の犬 (左から \(\frac{N+1}{2}\) 番目の犬) と中央の猫 (左から \(\frac{M+1}{2}\) 番目の猫) は隣接する
2. 中央の犬/猫には、それぞれの種族内で不満係数が最大のものが割り当てられる
3. 中央の犬&猫の両端にある列は、中央に近づくほど不満係数が高くなるように並んでいる

1. 中央の犬と中央の猫は隣接する

中央の犬と中央の猫の間に他の動物が入っている場合は、

この図のように、元々間に挟まっていた犬は中央の猫の横に、元々間に挟まっていた猫は中央の犬の横に追い出す操作を考えましょう。この操作によって偏りが増加する動物はいないため、解は悪化しません。よって、最適解において中央の犬と中央の猫は隣接するとして良いです。

2. 中央の犬/猫には、それぞれの種族内で不満係数が最大のものが割り当てられる

中央の犬と中央の猫が隣接しているとき、中央の犬/猫の偏りはどちらも \(1\) で、これは偏りの最小値ですから、不満係数最大のものを割り当てるのが最適です（並び替え不等式）。

3. 中央の犬&猫の両端にある列は、中央に近づくほど不満係数が高くなるように並んでいる

各列の中で隣接する \(2\) 匹の動物であって、中央に近いものの方が不満係数が小さいようなペアがあったとします。このペア内で順序を入れ替えた場合、

• \(2\) 匹がどちらも犬またはどちらも猫ならば、偏りは変化しないので、不満度も変化しません。
• \(2\) 匹のうち一方が犬で他方が猫ならば、元々中央に近かった方の偏りが \(2\) 増加し、他方の偏りが \(2\) 減少します。不満係数の大小関係に関する仮定から、不満度の総和は減少します。

よって、不満係数の大小が逆転している隣接ペアがある限りそのペア内で順序を入れ替えることによって、解を悪化させることなく「中央に近づくほど不満係数が高くなるように並んでいる」状態にすることができます。

\(N\) が奇数、\(M\) が偶数の場合

中央の犬が左から \(\frac{M}{2}\) 番目の猫と \(\frac{M}{2}+1\) 番目の猫の間にいない場合、

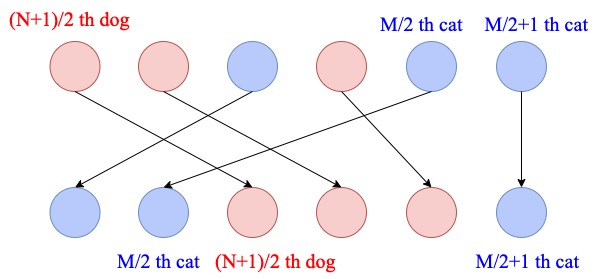
このような操作をしても解は悪化しません。あとは \(N\) が奇数、\(M\) が奇数の場合と同様に示せます。

\(N\) が偶数、\(M\) が偶数の場合

同様に、下図のような操作を考えます。

左から \(\frac{N}{2}\) 番目の犬、\(\frac{N}{2}+1\) 番目の犬、\(\frac{M}{2}\) 番目の猫、\(\frac{M}{2}+1\) 番目の猫の \(4\) 匹だけを取り出して位置関係を考えたとき、上の操作によって「犬犬猫猫」「猫猫犬犬」のパターンはなくなり、「犬猫犬猫」「猫犬猫犬」「犬猫猫犬」「猫犬犬猫」の \(4\) 択になります。いずれにせよ、全体の左半分 \(\frac{N+M}{2}\) 匹の中には犬 \(\frac{N}{2}\) 匹と猫 \(\frac{M}{2}\) 匹が含まれるので、全体の左半分と右半分それぞれについて \(N\) が奇数、\(M\) が奇数の場合の 3. と同様の議論が回ります。

2. 求値

\(N\) や \(M\) が奇数の場合は、中央の動物を適切な前処理の上除いておくことで \(N\) も \(M\) も偶数の場合に帰着できます。

以下、 \(N\) も \(M\) も偶数の場合を考えます。上述したとおり、最適解を与える列として考える必要があるのは以下のものに限られます。

• \(\frac{N}{2}\) 匹の犬と\(\frac{M}{2}\) 匹の猫を不満係数の昇順に並べた \(2\) つの列 \(P,Q\) に対して、\(P\) と「\(Q\) を反転した列」をつなげたもの (ただし、それぞれの動物は \(P\) と \(Q\) のどちらか一方のみに現れる)。

よって、\(N+M\) 匹の動物を不満係数の昇順に見ていきながら、順に \(P\) または \(Q\) の末尾に追加していく動的計画法をすれば良いです。

具体的には、

\[\mathrm{dp}[i][j][k] = \text{不満係数の昇順に i 匹見て、P の中に犬が j 匹・猫が k 匹含まれるときの不満度の総和の最小値}\]

と定義すると、\(i,j,k\) の値から新しく追加する動物の偏りが計算でき、 \(O(1)\) で遷移可能です。\(\mathrm{dp}[N+M][\frac{N}{2}][\frac{M}{2}]\) が求める答えになります。

計算量は \(O(NM(N+M))\) です。

追記 : \(O((N+M)\log (N+M ))\) で解けるようです (tatyamさんによる予想、noshiさんによる証明)。

想定解 (C++) :

#include<bits/stdc++.h>

using namespace std;

using ll = long long;

void chmin(ll &a, ll b) {
    a = min(a, b);
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n), b(m);
    for (int &i: a) cin >> i;
    for (int &i: b) cin >> i;
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    ll ans = 0;
    if (n & 1) {
        if (m & 1) ans += a.back();
        ans += accumulate(b.begin(), b.end(), 0LL);
        a.pop_back();
        --n;
    }
    if (m & 1) {
        ans += accumulate(a.begin(), a.end(), 0LL);
        b.pop_back();
        --m;
    }
    // pair の第 1 引数 : A_i または B_i
    //        第 2 引数 : 犬ならば 0、猫ならば 1
    vector<pair<int, int>> v;
    for (int i = 0; i < n; i++) v.emplace_back(a[i], 0);
    for (int i = 0; i < m; i++) v.emplace_back(b[i], 1);
    sort(v.begin(), v.end());
    
    vector dp(n + m + 1, vector(n + 1, vector<ll>(m + 1, 1LL << 60)));
    dp[0][0][0] = 0;
    int dog = 0, cat = 0;
    for (int i = 0; i < n + m; i++) {
        ll now = v[i].first;
        if (v[i].second == 0) {
            for (int j = 0; j <= dog; j++) {
                for (int k = 0; k <= cat; k++) {
                    chmin(dp[i + 1][j + 1][k], dp[i][j][k] + now * (m - k * 2));
                    chmin(dp[i + 1][j][k], dp[i][j][k] + now * (m - (cat - k) * 2));
                }
            }
            ++dog;
        } else {
            for (int j = 0; j <= dog; j++) {
                for (int k = 0; k <= cat; k++) {
                    chmin(dp[i + 1][j][k + 1], dp[i][j][k] + now * (n - j * 2));
                    chmin(dp[i + 1][j][k], dp[i][j][k] + now * (n - (dog - j) * 2));
                }
            }
            ++cat;
        }
    }
    ans += dp[n + m][n / 2][m / 2];
    cout << ans << endl;
}