Ex - add 1 Editorial by kyopro_friends

問題は次のように読み替えられます。(数列 \(A\) は 0-indexed に読み替えます)

空の数列から始めて、末尾に \(0,1,\ldots,N-1\) のいずれかをランダムに \(1\) つ追加する。
数列の長さが \(A_{N-1}\) 以上かつ、全ての\(0\leq i < N\) について「数列の末尾から \(A_i\) 個以内に \(i\) が存在しない」という状態にしたい。
操作回数の期待値は？

マルコフ連鎖(もどき)を考えます。 状態 \(i\) を「\(i\) より大きな任意の数 \(k\) について、『数列の末尾から \(A_k-A_i\) 個以内に \(k\) が存在しない』という状態」とします。
(注：本当にマルコフ連鎖として考えるのであれば、ここで定義した状態 \(i\) は、このあと何度 \(i\) を出したかによってさらに細かい状態に分けるべきですが、下図を参照して文脈から適切に補完して読んでください)
例えば \(A=(0,2,5,6)\) のとき、数列が \((2,3,0,1,0,1)\) であれば、これは状態 \(1\) です。

図

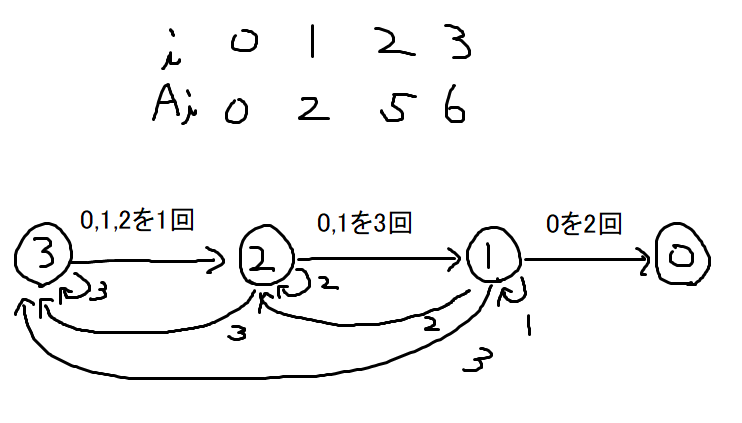
\(0\) に関する条件は自動的に満たされることから、状態 \(N-1\) から始めて状態 \(0\) に到達するまでの期待値を求める問題になりました。

状態 \(i+1\) からの遷移は

  • \(i\) 以下の数を \(A_{i+1}-A_i\) 回連続して出すと 状態 \(i\) へ
  • \(i\) より大きな数 \(k\) を出すと状態 \(k\) へ

となります。

状態 \(i\) から状態 \(0\) に遷移するまでの操作回数の期待値を \(E_i\) とします。状態 \(i+1\) からの遷移先は状態 \(i,i+1,\ldots,N\) なので、\(E_{i+1}\) は \(E_i,E_{i+1},\ldots,E_N\) の一次式で表せることがわかります。この式を \(E_i\) について解くことで、添字の大きい方から順に \(E_i\) を \(E_N\) の一次式で表すことができます。したがって、\(E_0\) と \(E_N\) の関係から \(E_N\) を求めることができます。これには一見 \(\Omega(N^2)\) 必要なように見えますが、実は \(O(N+\log A)\) で求めることができます。

具体的に詳しく計算してみましょう。状態 \(N-i\) から状態 \(N-(i+1)\) への遷移を考えてみます。\(p_i=\frac{N-i}{N}, c_i=A_{N-i}-A_{N-(i+1)}\) とします。このとき

\[E_{N-i}=\sum_{k=1}^{c_i}\sum_{m=1}^{i}\frac{1}{N}p_i^{k-1}(E_{N-m}+k)+p_i^{c_i}(E_{N-(i+1)}+c_i)\]

となります。第 \(1\) 項は、\(k\) 回目の操作で状態 \(N-m\) に遷移するケース、第 \(2\) 項は \(c_i\) 回の操作を無事終えて状態 \(N-(i+1)\) に遷移するケースを表します。この式を整理することで

\[-p_i^{c_i}E_{N-(i+1)}=\frac{1}{N}\frac{1-p_i^{c_i}}{1-p_i}\sum_{m=1}^{i}E_{N-m}+\frac{1}{1-p_i}(1-(c_i+1)p_i^{c_i}+c_ip_i^{c_i+1})+c_ip_i^{c_i}-E_{N-i}\]

を得ます。したがって、\(E_{N-m}\) の累積和を求めておくことでこれは高速に求めることができます。

数式の両辺に登場する \(E_*\) の係数をよく比べることで、 \(E_i=X_iE_N+Y_i\) と表したとき、任意の \(i\) で \(X_i=1\) となることが帰納法によりわかります(※上で記述した”整理する前の式”の両辺に登場する \(E_*\) の係数の和がそれぞれ \(1\) であることを用いると簡単に証明できます)。よって、上式の計算の過程において分母にくる数は \(N\) 以下の数の累乗のみであり、制約の範囲内において \(0\) 除算はおこりません。また、特に、実装上は \(Y_i\) のみを計算すれば十分です。

実装例(C++)
実装例(Python)

類題：

posted:
last update: