This problem can be solved in an \(O(N^2)\) times with DP (Dynamic Programming) where \(dp[\) the \(i\)-th day has ended \(][\) he possesses \(j\) unit of stock \(]=\{\) maximum amount of money he gains \(\}\). Since there is no use in keeping some stock when on the last day, the answer is \(dp[N][0]\).

Let us observe this DP with Sample 1.

Input of Sample 1:

8
2 5 4 3 7 1 8 6

The DP table where the \(i\)-th row from the top and \((j-1)\)-th column from the left contains \(dp[i][j]\):

 0  -2
 3  -2  -7
 3  -1  -6 -11
 3   0  -4  -9 -14
 7   3  -2  -7 -14 -21
 7   6   2  -3  -8 -15 -22
14  10   5   0  -7 -14 -22 -30
16  11   6   0  -6 -13 -20 -28 -36

We can observe some arithmetic progressions horizontally, so let’s find the differences between adjacent terms.
Here is a table where the \(i\)-th row from the top and \((j-1)\)-th column from the left contains \(dp[i][j-1]-dp[i][j]\):

2
5 5
4 5 5
3 4 5 5
4 5 5 7 7
1 4 5 5 7 7
4 5 5 7 7 8 8
5 5 6 6 7 7 8 8

Observing this table to find \(dp[N][0]\), the following solution seems to be valid:

• First, prepare a multiset \(M=\{A_1\}\), and initialize the answer \(R\) with \(0\).
• For each \(i=2,3,\dots,N\) in this order, do the following:
  • If \(A_i\) is greater than the minimum value \(m\) of \(M\), then add \(A_i-m\) to \(R\) and remove (one) \(m\) from \(M\). Then, insert two \(A_i\)’s to \(M\).
  • Otherwise, insert one \(A_i\) to \(M\).

Actually, this solution is correct. We will now justify the solution.

Consider a zig-zag line where the horizontal axis represents \(j\) and the vertical axis represents \(dp[i][j]\). Assume that this zig-zag line is always concave. (As of \(dp[1]\), this is obviously correct.)
Consider the transition from \(dp[i]\) to \(dp[i+1]\).
\(dp[i+1][j]\) is the \(\max\) of the following three values:

• \(dp[i][j]\) (If he does nothing on the \((i+1)\)-th day)
• \(dp[i][j-1]-A_{i+1}\) (If he buys a unit of stock on the \(i+1\)-th day)
• \(dp[i][j+1]+A_{i+1}\) (If he sells a unit of stock on the \(i+1\) th day)

These correspond to translations of the zig-zag line as follows:

• \(dp[i]\) (let us denote this by \(dp\))
• \(dp[i]\), shifted \(1\) unit in the right and \(A_{i+1}\) downwards (let us denote this by \(dp_-\))
• \(dp[i]\), shifted \(1\) unit in the left and \(A_{i+1}\) upwards (let us denote this by \(dp_+\))

The figure below illustrates the zig-zag lines corresponding to the transition from \(dp[6]\) to \(dp[7]\) when \(A=(4,2,2,1,1,1,3)\).

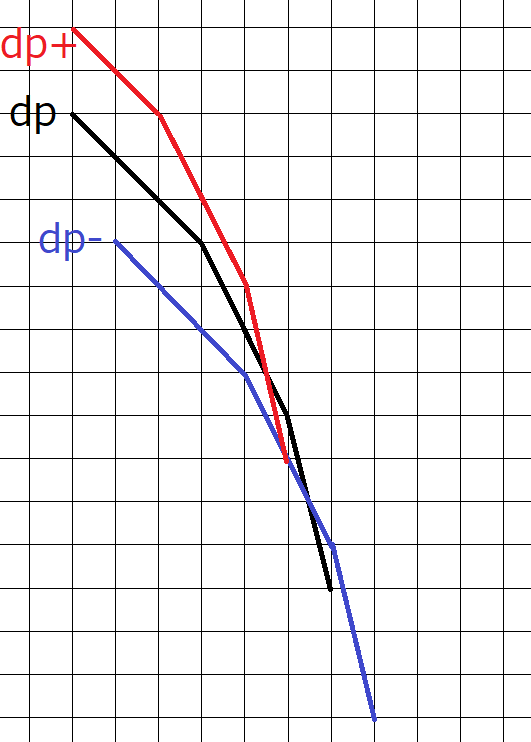
Let us first compare \(dp\) and \(dp_-\) to consider the zig-zag line \(L_-\) of their \(\max\):

• In the fraction where the slopes of both polylines are greater than or equal to \(-A_{i+1}\), \(dp\) is above or coincides with \(dp_-\), so \(L_-\) coincides with \(dp\).
• In the fraction where the slopes of both polylines are less than \(-A_{i+1}\), \(dp_-\) is above \(dp\), so \(L_-\) coincides with \(dp_-\).
• Between these two fractions, there is a segment of slope \(-A_{i+1}\) (with width \(1\)) on the polyline \(L_-\). This is where \(dp_-\) surpasses \(dp\).

Let us next consider the zig-zag line \(L_+\) by comparing \(dp\) and \(dp_+\):

• In the fraction where the slopes of both polylines are greater than or equal to \(-A_{i+1}\), \(dp_+\) is above or coincides with \(dp\), so \(L_+\) coincides with \(dp_+\).
• In the fraction where the slopes of both polylines are less than \(-A_{i+1}\), \(dp\) is above \(dp_+\), so \(L_+\) coincides with \(dp\).
• Between these two fractions, there is a segment of slope \(-A_{i+1}\) (with width \(1\)) on the polyline \(L_+\). This is where \(dp\) surpasses \(dp_+\).

The \(dp\) after the final transition is \(\max\) of \(L_-\) and \(L_+\), so it can be obtained by inserting a segment of slope \(-A_{i+1}\) and width \(1\) or \(2\) and shifting appropriately.

From the discussion above, we can derive the justification of the solution we described.

Sample code (C++):

#include<bits/stdc++.h>

using namespace std;

int main(){
  int n;
  cin >> n;
  vector<long long> a(n);
  for(auto &nx : a){cin >> nx;}
  long long res=0;
  priority_queue<long long,vector<long long>,greater<long long>> pq;
  pq.push(a[0]);
  for(int i=1;i<n;i++){
    if(pq.top()<a[i]){
      res+=(a[i]-pq.top());
      pq.pop();
      pq.push(a[i]);
    }
    pq.push(a[i]);
  }
  cout << res << '\n';
  return 0;
}