この問題は群ラベル付きグラフにおける単一始点最短非零パス問題の特殊ケースと見なせ，後者の問題は一般に \(\mathrm{O}(M \log N)\) 時間で解けます． 群と言っても，今回は非負整数の排他的論理和 (XOR) で十分なので，その場合に限定して説明します． （一般論に興味がある方はこちらをご覧ください．）

通常の最短路問題では辺に長さ（非負）が付いたグラフが入力として与えられますが，最短非零パス問題ではさらにラベルと呼ばれる非負整数が（長さとは無関係に追加で）辺に付いているとします． また，辺は無向（双方向に通れる）とします． そして，「単純パス（同じ頂点を複数回通らない経路）であって，通る辺のラベルの総 XOR が \(0\) でないものに限定する」という制約条件の下で，通常通り「通る辺の長さの総和を最小化する」ことを目指します．

元の問題を上記の問題として定式化してみましょう．（下図参照）

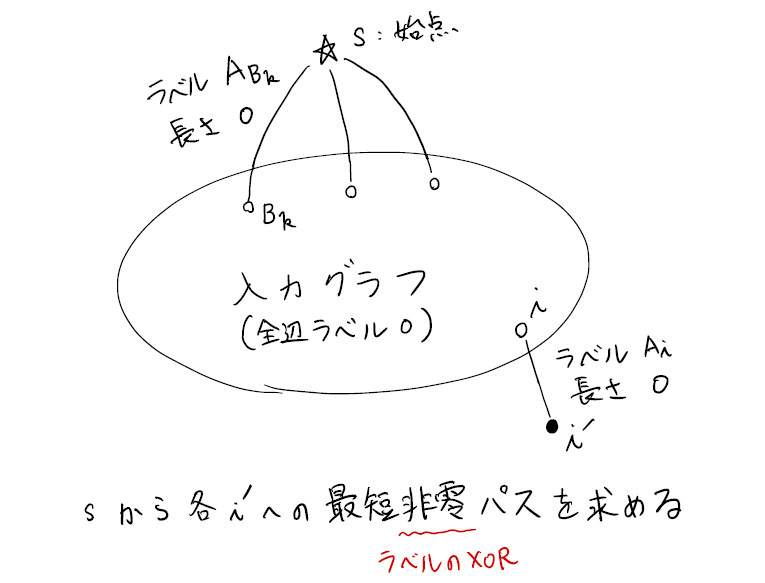
• まず，元の問題の入力グラフをそのまま使うことにして，各辺のラベルを \(0\) に設定します．
• 次に，単一始点にするための超始点 \(s\) を導入して，各人気者 \(B_k\) \((k = 1, 2, \dots, L)\) に対して新しく辺 \(\{s, B_k\}\) を追加し，その長さを \(0\) に，ラベルを所属国 \(A_{B_k}\) に設定します．
• 最後に，各人 \(i = 1, 2, \dots, N\) に対して新しく頂点 \(i'\) と辺 \(\{i, i'\}\) を追加し，その長さを \(0\) に，ラベルを所属国 \(A_i\) に設定します．

このグラフで \(s\) から各 \(i'\) への最短非零パスの長さを計算できれば，その値が \(i\) に関して求めたい答えとなっています． これは，同じ国の人気者から到達する場合，またその場合に限り，国由来のラベルが XOR で打ち消し合って \(0\) となることから従います．

XOR での単一始点最短非零パス問題の一般形は yukicoder No.1602 “With Animals into Institute 2” として公開されており，こちらの AC コードに上で構成したようなグラフを入力すれば，本問題でも AC を得ることができます．（アルゴリズムの中身に興味がある方はそちらの解説もご覧ください．）

実践例 (C++, 285 ms)

なお，本問題のために上で構成したグラフでは，始点・終点周りにしか非零ラベルの辺が存在しないため，始点・終点周りの追加辺の長さを \(0\) ではなく十分大きい整数に設定することで，「単純パスであれ」という制約条件を実質的に無視することができます． これにより始点・終点周りの辺はそれぞれ \(1\) 回しか使えなくなり，かつ，元のグラフの中でいくら迂回してもラベルは一切変わらないため，最短非零パス長＝最短非零ウォーク（同じ頂点を複数回通ってもよい経路）長となるからです． 一般の群ラベル付きグラフであっても，後者を求めるのは公式解説にあるような Dijkstra 法の素朴な拡張（ \(2\) 種類目までのラベルと最短経路長を管理する DP ）により可能です．