This is a translation of a user’s editorial

---

Notations

For a positive integer \(N\) and a prime \(p\), let \({\rm ord}_p(N)\) be the number of times that \(N\) divides \(p\).

By decomposing into products of exponents of primes, the original problem can be written as follows.

Problem (☆): Given a prime \(p\), positive integers \(e\) and \(K\), an integer \(N\) between \(0\) (inclusive) and \(p^e\) (exclusive), and a positive integer \(\rm MOD\), find the number, modulo \(\rm MOD\), of sequences \(A\) of length \(K\) consisting of integers between \(0\) (inclusive) and \(p^e\) (exclusive) such that \(\prod A_i =N \bmod p^e\).

In fact, this problem can be solved if the following problem is solved.

Problem (★): Given a prime \(p\), positive integers \(e\) and \(K\), and a positive integer \(\rm MOD\), find the number, modulo \(\rm MOD\), of sequences \(A\) of length \(K\) consisting of integers between \(0\) (inclusive) and \(p^e\) (exclusive) such that \(\prod A_i = p^x \bmod p^e\), for each \(x=0,\ldots,e-1\).

We will prove that Problem (★) and Problem (☆) can be solved in a total of \(O(e+\log K)\) (see notes). Hereinafter, unless otherwise noted, \(A\) will denote “a sequence of length \(K\) consisting of integers between \(0\) (inclusive) and \(p^e\) (exclusive).”

Notes

• We assume that \((e-1)!\) and \(\rm MOD\) are coprime.
• We assume that the arithmetic operation modulo \(\rm MOD\) can be done in an \(O(1)\) time. If \(p\) and \(K\) are enormous, an additional cost of finding the remainder by \(\rm MOD\) is imposed.
• When solving Problem (☆), in addition to the time required solve Problem (★), additional time of finding \({\rm ord}_p(N)\) is imposed too. This requires \(O(e)\) number of multiplications and divisions in which \(N\) and \(p\) concerns.

Problem (☆) can be solved if Problem (★) can be solved

We will first show the following claim.

Claim(◆): If integer \(X\) and \(Y\) satisfies \({\rm ord}_p(X)={\rm ord}_p(Y)< e\), then the number of sequences such that \(\prod A_i =X\bmod p^e\) and that of \(\prod A_i =Y\bmod p^e\) are equal.

Proof

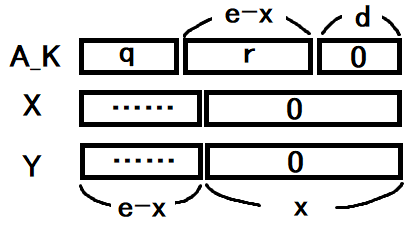
Take an arbitrary \(x\) such that \(0\leq x< e\) and positive integers \(X\) and \(Y\) such that \({\rm ord}_p(X)={\rm ord}_p(Y)=e\). Take an arbitrary integer sequence such that \(\prod A_i =X\bmod p^e\). With a positive integer \(r\) that are coprime with \(p\) and less than \(p^{e-x}\) and an integer \(q\), we can uniquely express as \(A_K=p^d(qp^{e-x}+r)\). Here, let \(r'\) be the only integer less than \(p^{e-x}\) such that \(\frac{Y}{p^x}r=\frac{X}{p^x}r' \bmod p^{e-x}\). By replacing \(A_k\) with \(p^d(qp^{e-x}+r')\), the resulting sequence satisfies \(\prod A_i =Y\bmod p^e\). By the construction of \(r'\), this transformation is bijective. (Q.E.D.)

Intuitive explanation

When written in base \(p\), \(X\) and \(Y\) has \(e-x\) digits except for trailing zeros. By adjusting the last \(e-x\) digits (except for the trailing zeros) of \(A_K\), any product can be obtained as long as \({\rm ord}_p\) remains the same.

Once Problem (★) is solved, Problem (☆) can be solved as follows.

• When \(N\neq 0\), the answer of Problem (★) for \(x={\rm ord}_p(N)\) is the desired value itself.
• When \(N=0\), the answer is the size of the universal set \((p^e)^K\) subtracted by the number of cases where \({\rm ord}_p(\prod A_i)< e\). It can be obviously found in an \(O(e+\log K)\) time.

Solving Problem (★)

The desired answer is \(\binom{K+x-1}{x}(p-1)^{K-1} p^{(e-1)(K-1)}\).

Proof

The number of integers \(n\) between \(0\) (inclusive) and \(p^e\) (exclusive) such that \({\rm ord}_p(n)=x\) is \((p-1)p^{e-1-x}\). Therefore, by Claim (◆), it is sufficient to prove that there are \(\binom{K+x-1}{x}(p-1)^K p^{(e-1)K-x}\) sequences such that \({\rm ord}_p(\prod A_i)=x\). Consider the sequence \(c\) such that \(c_i={\rm ord}_p(A_i)\). Since \({\rm ord}_p(\prod A_i)=x\) if and only if \(\sum c_i=x\), we will first take an arbitrary sequence \(c\) of non-negative integers such that \(\sum c_i=x\), and then take \(A_i\) such that \(c_i={\rm ord}_p(A_i)\). Once \(c\) is determined, for each \(i\) there are \((p-1)p^{e-1-c_i}\) possible values of \(A_i\) (since \(c_i < e\)), so there are \(\prod (p-1)p^{e-1-c_i}=(p-1)^K p^{(e-1)K-x}\) possible sequences for \(A\) such that \(c_i={\rm ord}_p(A_i)\), which is independent of \(c\). Since there are \(\binom{K+x-1}{x}\) possible \(c\), the sought count is \(\binom{K+x-1}{x}(p-1)^K p^{(e-1)K-x}\).

Illustration

By computing the binomial coefficients while finding the inverses in \(O(1\)) time each in the increasing order of \(x\), the entire computation can be completed in a total of \(O(\log K+e)\) time.

Also, if \(\rm MOD\) is an integer, by precalculating \(K\bmod ({\rm MOD}-1)\), \(O(\log K)\) can be reduced to \(O(\log\min\{K,{\rm MOD}\})\).

Hence, for example, the problem can also be solved for the following constraints.

Constraints

• \(M=p^m,N=p^n\); \(p\), \(n\), and \(m\) are given instead of \(N,M\).
• \(1 \leq K \leq 10^{1000000}\)
• \(2 \leq p \leq 10^{1000000}\)
• \(p\) is a prime.
• \(0 \leq n < m \leq 10^{6}\)